
 ��ͼ����ʾ��ƽ�н�����A��B��ľ���Ϊd������A��B���ϼ�����ͼ����ʾ�ķ�����ѹ��t=0ʱA���B��ĵ��Ƹߣ���ѹ������ֵΪU0������ֵҲΪU0����������Ϊm����Ϊ+q��������ɵ�����������AB���е�O�ؽ�����������OO�����ٶ�v0=$\frac{{q{U_0}T}}{3md}$�������룬����������AB��ķ���ʱ���ΪT����������Ӱ�죮����
��ͼ����ʾ��ƽ�н�����A��B��ľ���Ϊd������A��B���ϼ�����ͼ����ʾ�ķ�����ѹ��t=0ʱA���B��ĵ��Ƹߣ���ѹ������ֵΪU0������ֵҲΪU0����������Ϊm����Ϊ+q��������ɵ�����������AB���е�O�ؽ�����������OO�����ٶ�v0=$\frac{{q{U_0}T}}{3md}$�������룬����������AB��ķ���ʱ���ΪT����������Ӱ�죮�������� ��1������ţ�ٵڶ����ɣ�����˶�ѧ��ʽ���t=0ʱ����Ĵ���������������ƫת���룻
��2�������ڴ�����ӵ��ٶȶ�����ͬ�ģ����ٶȺϳɷ���⣻
��3��Ҫʹƽ�������ܹ�����Բ�δų�����߽�������С����ʱ���ų�ֱ����Сֵ�����ӿ�����ȣ����ɵõ��ų��������С�뾶�����ӽ�����ǿ�ų��У������������ṩ����������ţ�ٵڶ����������Ӧ�ĴŸ�ǿ�ȣ�
��� �⣺��1����������t=0ʱ�̽���糡������ƫת����Ϊ��
${s_1}=\frac{1}{2}a{��\frac{2T}{3}��^2}+a��{\frac{2T}{3}}��•\frac{T}{3}-\frac{1}{2}a{��\frac{T}{3}��^2}$$a=\frac{{q{U_0}}}{md}$
��ã�${s_1}=\frac{{7q{U_0}{T^2}}}{18md}$
��2��������ӵ��ٶȶ�����ͬ�ģ����ص糡�߷����ٶȴ�СΪ��${v_y}=a•\frac{T}{3}$
���Դ���ٶȴ�СΪ��$v=\sqrt{v_0^2+v_y^2}$
��ã�$v=\frac{{\sqrt{2}q{U_0}T}}{3md}$
���ٶȷ�����v0�ļн�Ϊ�ȣ����У�$tan��=\frac{{v}_{y}}{{v}_{0}}=1$��
����=45��
��3����������t=nTʱ�̽���糡������ƫת�������Ϊ��${s_1}=\frac{{7q{U_0}{T^2}}}{18md}$��
��������$t=nT+\frac{2T}{3}$ʱ�̽���糡������ƫת�������Ϊ��${s_2}=\frac{{q{U_0}{T^2}}}{18md}$��
���ԣ��ھ���O���е��·�$\frac{{7q{U_0}{T^2}}}{18md}$���Ϸ�$\frac{{q{U_0}{T^2}}}{18md}$��Χ�������Ӵ���� ������������糡ʱ���ٶȷ���˴�ƽ�У�Ҫʹƽ�������ܹ�����Բ�δų�����߽�������С����ʱ���ų�ֱ����Сֵ�����ӿ�����ȣ�
������������糡ʱ���ٶȷ���˴�ƽ�У�Ҫʹƽ�������ܹ�����Բ�δų�����߽�������С����ʱ���ų�ֱ����Сֵ�����ӿ�����ȣ�
���ӿ���Ϊ��D=��s1+s2��cos45��
�ʴų��������С�뾶Ϊ��$r=\frac{D}{2}=\frac{{\sqrt{2}q{U_0}{T^2}}}{9md}$
�����ڴų�����Բ���˶����У�$qvB=m\frac{v^2}{r}$
��ã�$B=\frac{3m}{qT}$��
�𣺣�1��t=0ʱ����Ĵ���������������ƫת����Ϊ$\frac{7q{U}_{0}{T}^{2}}{18md}$��
��2����������糡ʱ���ٶ�Ϊ$\frac{\sqrt{2}q{U}_{0}T}{3md}$��
��3���ų��������С�뾶Ϊ$\frac{\sqrt{2}q{U}_{0}{T}^{2}}{9md}$����Ӧ�ĴŸ�ǿ����$\frac{3m}{qT}$��
���� ���⿼���˴��������ڵ糡�ʹų��е��˶������մ�����ƽ���˶��ķ������Լ�֪�����ӽ���ų���������Բ���˶������ü���֪ʶ����뾶��


 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
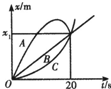 A��B��C��������ͬʱͬ�س�����ֱ���˶������ǵ�x-tͼ����ͼ��ʾ����20s��ʱ���ڣ����ǵ�·�̹�ϵ��A��·�����BC��ȣ�
A��B��C��������ͬʱͬ�س�����ֱ���˶������ǵ�x-tͼ����ͼ��ʾ����20s��ʱ���ڣ����ǵ�·�̹�ϵ��A��·�����BC��ȣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���˶����ٶȴ�С���ڷ��˶����ٶȴ�С֮�� | |
| B�� | ��������ֱ���˶��ĺ��˶�һ��Ҳ������ֱ���� | |
| C�� | ���ɽǶȵ�һ������ֱ���˶���һ���ȱ���ֱ���˶��ĺ��˶���һ���������˶� | |
| D�� | �����˶��������˶���������˶���������һ���������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ͨ��Խ��Ӧ�綯��Խ����ԽС | |
| B�� | ��ͨ���仯Խ�࣬��Ӧ�綯��Խ�� | |
| C�� | ��ͨ���仯Խ�죬��Ӧ�綯��Խ�� | |
| D�� | ��ͨ��Ϊ��ʱ����Ӧ�綯��һ��Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | һ����ֱ���˶� | B�� | һ���������˶� | ||
| C�� | ������ֱ��Ҳ�����������˶� | D�� | ����˵��������ȷ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����˶�״̬�ı��ԭ�� | |
| B�� | ����ʹ����λ�Ʋ��������ԭ�� | |
| C�� | ������ֱ���˶�����������ܵ�ƽ���������� | |
| D�� | ֻҪ�����˶��켣������������Ȼ�ܵ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ����Ϊm�ķɻ���ˮƽ�ٶ�v0�����ܵ��������������ɻ��ڴ˹�����ˮƽ�ٶȱ��ֲ��䣬ͬʱ�ܵ���������ֱ���ϵĺ㶨���������������������ĺ����ṩ�����������������õ��ɻ���ˮƽ�����λ��ΪLʱ���������ĸ߶�ΪH����
����Ϊm�ķɻ���ˮƽ�ٶ�v0�����ܵ��������������ɻ��ڴ˹�����ˮƽ�ٶȱ��ֲ��䣬ͬʱ�ܵ���������ֱ���ϵĺ㶨���������������������ĺ����ṩ�����������������õ��ɻ���ˮƽ�����λ��ΪLʱ���������ĸ߶�ΪH�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com