
 如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,求:
如图所示,一质量为0.5kg的小球,用0.4m长的细线拴住在竖直面内作圆周运动,求:分析 小球在竖直平面内做圆周运动时,由重力和细线的拉力的合力提供小球的向心力,根据牛顿第二定律求出细线的拉力.
解答 解:(1)当小球在圆上最高点时,根据牛顿第二定律得:
F1+mg=m$\frac{{{v}_{1}}^{2}}{r}$
得到 F1=m$\frac{{{v}_{1}}^{2}}{r}$-mg=0.5($\frac{{4}^{2}}{0.4}$-10)N=15N,
(2)当小球在圆下最低点时,
F2-mg=m$\frac{{{v}_{2}}^{2}}{r}$
得到 F2=mg+m$\frac{{{v}_{2}}^{2}}{r}$=0.5(10+$\frac{(4\sqrt{2})^{2}}{0.4}$)N=45N.
答:(1)当小球在圆上最高点速度为4m/s时,细线的拉力是15N;
(2)当小球在圆下最低点速度为4$\sqrt{2}$m/s时,细线的拉力是45N.
点评 对于圆周运动动力学问题,关键是分析受力情况,寻找向心力的来源.细线对小球只有拉力作用,与轻杆不同.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图,一关于y轴对称的导体轨道位于水平面内,磁感应强度为B的匀强磁场与平面垂直.一足够长,质量为m的直导体棒沿x轴方向置于轨道上,在外力F作用下从原点由静止开始沿y轴正方向做加速度为a的匀速加速直线运动,运动时棒与x轴始终平行.棒单位长度的电阻ρ,与电阻不计的轨道接触良好,运动中产生的热功率随棒位置的变化规律为P=ky${\;}^{\frac{3}{2}}$(SI).求:
如图,一关于y轴对称的导体轨道位于水平面内,磁感应强度为B的匀强磁场与平面垂直.一足够长,质量为m的直导体棒沿x轴方向置于轨道上,在外力F作用下从原点由静止开始沿y轴正方向做加速度为a的匀速加速直线运动,运动时棒与x轴始终平行.棒单位长度的电阻ρ,与电阻不计的轨道接触良好,运动中产生的热功率随棒位置的变化规律为P=ky${\;}^{\frac{3}{2}}$(SI).求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
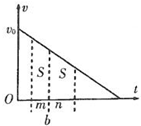 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,则b时刻速度vb的大小为( )| A. | $\frac{({m}^{2}+{n}^{2})S}{(m+n)mn}$ | B. | $\frac{mn({m}^{2}+{n}^{2})S}{(m+n)}$ | C. | $\frac{(m-n)S}{mn}$ | D. | $\frac{({m}^{2}+{n}^{2})S}{mn}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
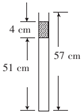 某物理兴趣小组为了探究气体实验定律,完成了如下的操作:该小组的同学将一截面积S=3cm2、长度L=57cm、一端封闭、粗细均匀导热性能良好的玻璃管竖直放置,如图所示.其中玻璃管竖直放置且开口向上,现将一段水银柱封闭玻璃管内的气体,经测量水银柱的长度为4cm,气柱的长度为51cm,已知环境温度为306K,外界的大气压强p0=76cmHg.
某物理兴趣小组为了探究气体实验定律,完成了如下的操作:该小组的同学将一截面积S=3cm2、长度L=57cm、一端封闭、粗细均匀导热性能良好的玻璃管竖直放置,如图所示.其中玻璃管竖直放置且开口向上,现将一段水银柱封闭玻璃管内的气体,经测量水银柱的长度为4cm,气柱的长度为51cm,已知环境温度为306K,外界的大气压强p0=76cmHg.查看答案和解析>>
科目:高中物理 来源: 题型:选择题

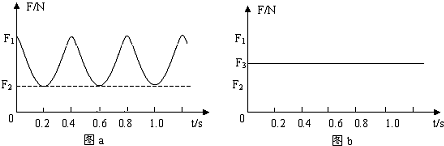
| A. | 振子沿如图的曲线运动 | |
| B. | 图象描述的是振子在任意时刻的位移 | |
| C. | 在0.5s到1.5s内振子先加速运动后减速运动 | |
| D. | 在1s到2s内振子先减速运动后加速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,光滑水平面上,有一个质量为M=3kg的木箱静止放置.木箱上某处静止有一小铁块,质量为M0=1kg,与木箱上表面间动摩擦因数为μ=0.2.在木箱右侧足够远的地方,放有一质量为m=9kg的薄板,其上表面为软胶体物质.木箱和薄板的上表面高度差为h=5m.某时刻,给小铁块一个水平向右的瞬时冲量I=4N•s,小铁块随即开始运动,刚好能“停”在木箱右边缘.之后的某时刻木箱与薄板发生极短时间的弹性碰撞,木箱顶部的小铁块顺势向前滑出,落到薄板上.(认为小铁块落到薄板上立即相对静止,不计空气阻力,薄板足够长,重力加速度g=10 m/s2).求:
如图所示,光滑水平面上,有一个质量为M=3kg的木箱静止放置.木箱上某处静止有一小铁块,质量为M0=1kg,与木箱上表面间动摩擦因数为μ=0.2.在木箱右侧足够远的地方,放有一质量为m=9kg的薄板,其上表面为软胶体物质.木箱和薄板的上表面高度差为h=5m.某时刻,给小铁块一个水平向右的瞬时冲量I=4N•s,小铁块随即开始运动,刚好能“停”在木箱右边缘.之后的某时刻木箱与薄板发生极短时间的弹性碰撞,木箱顶部的小铁块顺势向前滑出,落到薄板上.(认为小铁块落到薄板上立即相对静止,不计空气阻力,薄板足够长,重力加速度g=10 m/s2).求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com