
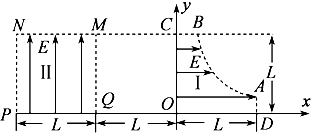
| A. | 从电场区域Ⅰ的边界B点(B点的纵坐标为L)处由静止释放电子,到达区域Ⅱ的M点时的速度为v=$\sqrt{\frac{eEL}{2m}}$ | |
| B. | 从电场区域Ⅰ的边界B(B点的极坐标为L)处由静止释放电子,电子离开MNPQ区域时的极坐标为(-2L,0) | |
| C. | 从电场区域Ⅰ的AB曲线上任一点处由静止释放的电子都能从MNPQ区域左下角P点离开 | |
| D. | 在电场区域Ⅰ的AB曲线上任一点处由静止释放的电子离开MNPQ区域时最小动能为2eEL |
分析 (1)根据B点的纵坐标求出B点的横坐标,根据动能定理求出电子到达区域Ⅱ的M点时的速度.
(2)电子进入电场II做类平抛运动,在垂直电场方向上做匀速直线运动,沿电场方向做匀加速直线运动,根据偏转位移的大小求出离开MNPQ时的纵坐标.
(3)根据动能定理,结合类平抛运动的规律求出在电场区域Ⅱ中偏转位移
解答 解:A、B点坐标($\frac{1}{4}L$,L),在电场I中电子被加速到V,由动能定理有:
$eE\frac{L}{4}=\frac{1}{2}m{v}^{2}$,
所以$v=\sqrt{\frac{eEL}{2m}}$,故A正确.
B、电子进入电场II做类平抛运动,有:
t=$\frac{L}{v}$;
$y=\frac{1}{2}a{t}^{2}$,
$a=\frac{eE}{m}$,
所以横坐标x=-2L;纵坐标y=L-y=0即为(-2L,0),故B正确
C、设释放点在电场区域I的AB曲线边界,其坐标为(x,y),在电场I中电子被加速到v1,然后进入电场II做类平抛运动,有:
$eEx=\frac{1}{2}{mv}_{1}^{2}$;
t=$\frac{L}{{v}_{1}}$;
$y′=\frac{1}{2}a{t}^{2}=\frac{1}{2}\frac{eE}{m}(\frac{L}{{v}_{1}})^{2}$;
所以离开点的横坐标X1=-2L,纵坐标y1=y-y′=0,即(-2L,0)为P点,故C正确
D、电子在两个电场中被加速,电场力做功为:W=eEx+eEy
则从B到P由动能定理得:eE(x+y)=Ek-0
又 y=$\frac{{L}^{2}}{4x}$,所以只有x=y点释放的电子,离开P点时动能最小,所以x+y=L,即最小动能为 EKmin=eEL,故D不正确.
因选不正确的,故选:D
点评 本题中电子先加速后偏转,基本方法是动能定理和运动的分解,难点在于数学知识的应用求极值和轨迹方程


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
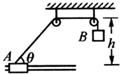 如图所示,跨过同一高度处的光滑定滑轮的细线连接着质量相同不计大小的物体A和B,A套在光滑水平杆上,B被托在紧挨滑轮处,细线与水平杆的夹角θ=30°,定滑轮离水平杆的高度h=0.2m.当B由静止释放后,求A所获得的最大速度.(sin53°=0.8,cos53°=0.6)
如图所示,跨过同一高度处的光滑定滑轮的细线连接着质量相同不计大小的物体A和B,A套在光滑水平杆上,B被托在紧挨滑轮处,细线与水平杆的夹角θ=30°,定滑轮离水平杆的高度h=0.2m.当B由静止释放后,求A所获得的最大速度.(sin53°=0.8,cos53°=0.6)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 原子核的结合能等于使其完全分解成自由核子所需的最小能量 | |
| B. | 核力具有饱和性 | |
| C. | 核力是短程力,可表现为引力也可表现为斥力 | |
| D. | 比结合能越大,原子核越不稳定 | |
| E. | 自由核子组成原子核时,其质量亏损所对应的能量大于该原子核的结合能 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 12s | B. | 6.2s | C. | 2.4s | D. | 1.1s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com