
 将比荷不同的离子分开,是原子核物理研究中的一项重要技术.一种方法是利用如图1所示的装置,在边界AC上方存在有区域足够大的方向垂直纸面向里的匀强磁场,磁感应强度为B,边界AC上有一狭缝.离子源放射出初速度可以忽略的正离子,离子进入电场并经电场加速后,穿过狭缝沿垂直于边界AC且垂直于磁场的方向射入磁场,最后打在置有离子接收器的区域CD上被收集.已知区域CD的右边界距狭缝的距离为L,左边界距狭缝足够远,整个装置内部为真空,不计离子重力,也不考虑离子间的相互作用.
将比荷不同的离子分开,是原子核物理研究中的一项重要技术.一种方法是利用如图1所示的装置,在边界AC上方存在有区域足够大的方向垂直纸面向里的匀强磁场,磁感应强度为B,边界AC上有一狭缝.离子源放射出初速度可以忽略的正离子,离子进入电场并经电场加速后,穿过狭缝沿垂直于边界AC且垂直于磁场的方向射入磁场,最后打在置有离子接收器的区域CD上被收集.已知区域CD的右边界距狭缝的距离为L,左边界距狭缝足够远,整个装置内部为真空,不计离子重力,也不考虑离子间的相互作用.分析 (1)每个离子加速获得能量为qU,根据能量守恒定律列式分析即可;
(2)离子在电场中加速,根据动能定理列式分析;在磁场中做匀速圆周运动,根据牛顿第二定律列式并结合几何关系分析;
(3)根据第二问中轨道半径与质量关系得到质量越大,轨道半径越大;画出临界轨迹,结合几何关系和牛顿第二定律,列式得到AC边上离子的宽度表达式进行分析.
解答 解:(1)设离子源单位时间内放射的离子数为n,根据功能关系,有:E=n•$\frac{1}{2}m{v}^{2}$=nqU,
即得离子源单位时间内放射的离子数为n=$\frac{E}{qU}$;
(2)正离子在电场中加速过程,有:
qU=$\frac{1}{2}m{v}^{2}$,
正离子在磁场中运动过程,有:
qvB=m$\frac{{v}^{2}}{r}$,
故r=$\frac{mv}{qB}=\sqrt{\frac{2mU}{q{B}^{2}}}$,
只要质量为m2离子能到达接收器的区域,所有的离子都能被收集,则加速电压U至少应满足:
2r2=L,
可解得:U=$\frac{q{B}^{2}{L}^{2}}{8{m}_{2}}$,
故加速电压U应该满足U≥$\frac{q{B}^{2}{L}^{2}}{8{m}_{2}}$;
(3)由r=$\frac{mv}{qB}=\sqrt{\frac{2mU}{q{B}^{2}}}$知,r与m的平方根成正比;
m1打到最近的是从狭缝右端以φ角入射,到狭缝左端的距离为2r1cosφ-d,
m2打到最远的是从狭缝左端垂直入射,到狭缝左端的距离为2r2,如图: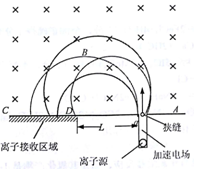
要将两种离子区分开,加速电压U至少应满足:
(2r1cosφ-α)-2r2=△s,
U=$\frac{q{B}^{2}(△s+α)^{2}}{8(\sqrt{{m}_{1}}cosφ-\sqrt{{m}_{2}})^{2}}$,
同理,要使离子能到达接收器的区域,则加速电压U至少应该满足:
2r2cosφ=L+d,
可解得:U=$\frac{q{B}^{2}(L+d)^{2}}{8{m}_{2}cosφ}$,
故加速电压U应该满足:
U≥$\frac{q{B}^{2}{(△s+α)}^{2}}{8{(\sqrt{{m}_{1}}cosφ-\sqrt{{m}_{2}})}^{2}}$,且U≥$\frac{q{B}^{2}{(L+d)}^{2}}{8{m}_{2}cosφ}$;
答:(1)此离子源单位时间内放射的离子数为$\frac{E}{qU}$;
(2)要使这两种离子都被收集,则加速电压U应满足U≥$\frac{q{B}^{2}{L}^{2}}{8{m}_{2}}$;
(3)加速电压U应满足U≥$\frac{q{B}^{2}{(△s+α)}^{2}}{8{(\sqrt{{m}_{1}}cosφ-\sqrt{{m}_{2}})}^{2}}$,且U≥$\frac{q{B}^{2}{(L+d)}^{2}}{8{m}_{2}cosφ}$.
点评 本题是离子在磁场中运动的问题,关键是明确离子在电场中是直线加速,在磁场中是匀速圆周运动,画出临界轨迹,结合动能定理和牛顿第二定律列式分析.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:计算题
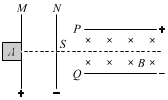 带电粒子的电荷量与质量的比值称为比荷,是描述带电粒子的重要参数.如图所示是某种测量带电粒子比荷实验的原理示意图,一对平行金属板M、N竖直放置,板间存在水平方向的匀强电场;另一对平行金属板P、Q水平放置,两板间距为d,板间存在竖直方向的匀强电场和垂直纸面向里的匀强磁场.在某次实验中,粒子源A不断产生某种带正电的粒子,带电粒子经金属板M、N间的电场加速,从N板上的小孔S射出,沿水平方向进入金属板P、Q间.调节电场和磁场,当M、N两板间的电势差为U1,P、Q两板间的电势差为U2,磁感应强度为B时,带电粒子在P、Q两板间恰好做匀速直线运动.粒子运动轨迹如图中虚线所示.设带电粒子离开粒子源时的速度、所受重力及粒子间的相互作用均可忽略.
带电粒子的电荷量与质量的比值称为比荷,是描述带电粒子的重要参数.如图所示是某种测量带电粒子比荷实验的原理示意图,一对平行金属板M、N竖直放置,板间存在水平方向的匀强电场;另一对平行金属板P、Q水平放置,两板间距为d,板间存在竖直方向的匀强电场和垂直纸面向里的匀强磁场.在某次实验中,粒子源A不断产生某种带正电的粒子,带电粒子经金属板M、N间的电场加速,从N板上的小孔S射出,沿水平方向进入金属板P、Q间.调节电场和磁场,当M、N两板间的电势差为U1,P、Q两板间的电势差为U2,磁感应强度为B时,带电粒子在P、Q两板间恰好做匀速直线运动.粒子运动轨迹如图中虚线所示.设带电粒子离开粒子源时的速度、所受重力及粒子间的相互作用均可忽略.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
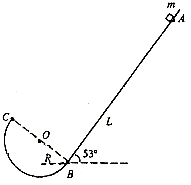 如图所示的绝缘轨道固定在竖直面内,其中,倾角53°的斜轨与半径R=0.2m的光滑半圆轨在B点相切,斜轨上A点有一可视为质点、质量m=0.1kg、电荷量q=1×10-3C的带正电滑块.己知A、B间距离L=1m,滑块与斜轨间的动摩擦因数μ=0.2,取g=10m/s2.
如图所示的绝缘轨道固定在竖直面内,其中,倾角53°的斜轨与半径R=0.2m的光滑半圆轨在B点相切,斜轨上A点有一可视为质点、质量m=0.1kg、电荷量q=1×10-3C的带正电滑块.己知A、B间距离L=1m,滑块与斜轨间的动摩擦因数μ=0.2,取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
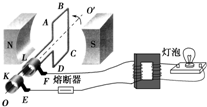 如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈线接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )
如图所示,50匝矩形闭合导线框ABCD处于磁感应强度大小B=$\frac{\sqrt{2}}{10}$T的水平匀强磁场中,线框面积S=0.5m2,线框电阻不计.线框绕垂直于磁场的轴OO′以角速度ω=200rad/s匀速转动,并与理想变压器原线圈相连,副线圈线接入一只“220V,60W”灯泡,且灯泡正常发光,熔断器允许通过的最大电流为10A,下列说法正确的是( )| A. | 变压器原、副线圈匝数之比为25:11 | |
| B. | 线框中产生交变电压的有效值为500$\sqrt{2}$V | |
| C. | 图示位置穿过线框的磁通量为零 | |
| D. | 允许变压器输出的最大功率为5000W |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )
如图所示,间距为l的两平行光滑金属导轨倾斜放置,匀强磁场垂直于导轨平面向上,将质量为m的导体棒放在导轨上,导体棒与导轨垂直且接触良好.当导体棒中通有从P到Q、大小为I的电流时,棒的加速度大小为a1;现将电流反向,其它条件不变,棒的加速度大小变为a2,若a1、a2均沿斜面向下,则该磁场的磁感应强度大小可表示为( )| A. | $\frac{{m(a}_{1}{+}_{{a}_{2}})}{2IL}$ | B. | $\frac{{m(a}_{1}{-}_{{a}_{2}})}{2IL}$ | C. | $\frac{{m(a}_{1}{+}_{{a}_{2}})}{IL}$ | D. | $\frac{{m(a}_{2}{-}_{{a}_{1}})}{2IL}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
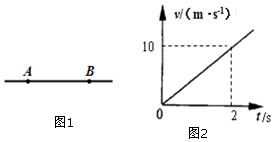 如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求:
如图,A、B是-条电场线上的两点,t=0时刻从A点释放一初速为零的电子,电子仅在电场力作用下,沿直线从A运动到B,其速度随时间变化的规律如图所示.t=2s时到达B点速度大小为10m/s.已知电子质量为m,电荷量大小为e.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
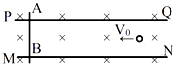 如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )
如图所示为某一装置的俯视图,PQ、MN为水平放置且足够长的平行金属薄板,两板间有磁感应强度为B的匀强磁场,方向垂直薄板平面向里,金属棒AB垂直放置在两板上且与两板接触良好.现有质量为m,电荷量为+q的粒子以初速度V0水平向左射入两板之间,若磁场足够大,粒子的重力不计,且粒子不会打到两板上,则( )| A. | 若带电粒子做匀速直线运动,则金属棒AB应向右运动 | |
| B. | 金属棒的速度为2 V0时,带电粒子可能做匀速直线运动 | |
| C. | 若金属棒的向左运动速度也为V0,则带电粒子一定做匀速直线运动 | |
| D. | 若金属棒一直未动,则带电粒子从初始时到位移大小为$\frac{m{V}_{0}}{qB}$时的时间间隔可能为t=$\frac{5πm}{3qB}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com