
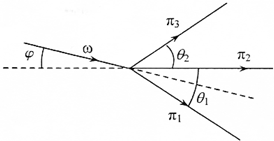
���� ��������ϵ�����������ֽ⣬�ֱ��x�����y�����ж�ά�˶��Ķ����غ㶨��
��� �⣺�Եڶ����н��ӵķ��з���Ϊx�ᣬ���¼�ƽ��Ϊx-yƽ�棬��˥��ǰ�ؽ��Ӻ�˥��������н��ӵĶ�����С�ֱ�ΪP����P1��P2��P3��˥��ǰ��������x��y������ܶ����ֱ��غ�
P��cos��=P1cos��1+P2+P3cos��2 ��
-P��sin��=-P1sin��1+P3sin��2 ��
˥��ǰ�������������غ�
m��c2+T��=��mc2+T1��+��mc2+T2��+��mc2+T3�� ��
ʽ����˺��Ҷ�����Բ������ʾ�����ֱ���˥��ǰ�ؽ��Ӻ�˥��������н��ӵ����ܣ������붯��֮�ͣ���˥��ǰ�ؽ��Ӻ�ˤ�������н��ӵ����ܿ����䶯���;�ֹ������ʾ����
T��=$\frac{{P}_{��}^{2}}{2{m}_{��}}$ ��
T1=$\frac{{P}_{1}^{2}}{2{m}_{\;}}$ ��
T2=$\frac{{P}_{2}^{2}}{2{m}_{\;}}$ ��
T3=$\frac{{P}_{3}^{2}}{2{m}_{\;}}$ ��
�ֱ��ɢݢޢ�ʽ��
P1=$\sqrt{2{mT}_{1}}$ ��
P2=$\sqrt{2{mT}_{2}}$ ��
P3=$\sqrt{2{mT}_{3}}$ ��
�ɢ٢ڢ���ʽ��
��=arctan$\frac{\sqrt{{T}_{1}}sin{��}_{1}-\sqrt{{T}_{3}}sin{��}_{2}}{\sqrt{{T}_{1}}cos{��}_{1}+\sqrt{{T}_{2}}+\sqrt{{T}_{3}}cos{��}_{2}}$⑪
P��=2m��T1+T2+T3��+4m[$\sqrt{{T}_{1}{T}_{3}}$cos����1+��2��+$\sqrt{{T}_{1}{T}_{2}}$cos��1+$\sqrt{{T}_{2}{T}_{3}}$cos��2]⑫
�ɢۢ�⑫ʽ��
2c2${m}_{��}^{2}$-2��3mc2+T1+T2+T3��m��+2m��T1+T2+T3��+4m[$\sqrt{{T}_{1}{T}_{3}}$cos����1+��2��+$\sqrt{{T}_{1}{T}_{2}}$cos��1+$\sqrt{{T}_{2}{T}_{3}}$cos��2]=0⑬
���Ϊm��=$\frac{3}{2}$m+$\frac{1}{2{c}^{2}}$��T1+T2+T3��+$\sqrt{[\frac{3}{2}m+\frac{1}{2{c}^{2}}��{T}_{1}+{T}_{2}+{T}_{3}��]^{2}-\frac{{P}_{��}^{2}}{2{c}^{2}}}$⑭ʽ�У�${P}_{��}^{2}$��⑫ʽ������
��һ��m����$\frac{{P}_{��}}{c}$���������۽�������m��c2����P��c ì�ܣ���ȥ��
�𣺦ؽ�����˥��ǰ��˲��ķ��з�����˥���ĵڶ������ӵķ��з���ļнǦ�Ϊarctan$\frac{\sqrt{{T}_{1}}sin{��}_{1}-\sqrt{{T}_{3}}sin{��}_{2}}{\sqrt{{T}_{1}}cos{��}_{1}+\sqrt{{T}_{2}}+\sqrt{{T}_{3}}cos{��}_{2}}$��
�ؽ��ӵľ�ֹ����Ϊ$\frac{3}{2}$m+$\frac{1}{2{c}^{2}}$��T1+T2+T3��+$\sqrt{[\frac{3}{2}m+\frac{1}{2{c}^{2}}��{T}_{1}+{T}_{2}+{T}_{3}��]^{2}-\frac{{P}_{��}^{2}}{2{c}^{2}}}$������${P}_{��}^{2}$��⑫ʽ��������
���� ���⿼���ά�˶��Ķ����غ㶨�ɣ�Ҫ���������ֽ⣬�ֱ���x�����y�����ж����غ㣬����֮�Ҫ�����������ܷ��̵����á������Ͷ���֮��Ļ����Լ������Ǻ�����ʹ�ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ֱ���� | B�� | ��б������ | C�� | ��б������ | D�� | ��ֱ��б������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
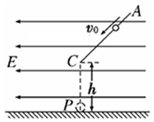 ��ͼ��ʾ����ˮƽ�������ǿ�糡����һ����⻬����ˮƽ���45��ǵľ�Եֱ��AC�����¶ˣ�C�ˣ������߶�h=0.8m����һ����Ϊ500g�Ĵ���С������ֱ���ϣ�����ijһ�ٶ��ظ������»���С����˺�����ͨ��C�˵����·�P�㴦����g=10m/s2��
��ͼ��ʾ����ˮƽ�������ǿ�糡����һ����⻬����ˮƽ���45��ǵľ�Եֱ��AC�����¶ˣ�C�ˣ������߶�h=0.8m����һ����Ϊ500g�Ĵ���С������ֱ���ϣ�����ijһ�ٶ��ظ������»���С����˺�����ͨ��C�˵����·�P�㴦����g=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | t1��t2ʱ��������һ���ڼ����½� | |
| B�� | t1��t2ʱ��������һ���ڼ������� | |
| C�� | t2��t3ʱ����������һ�����������˶�״̬ | |
| D�� | t2��t3ʱ�������������ܴ��ھ�ֹ״̬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
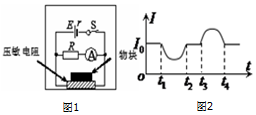
 �ס���������ȫ��ͬ�Ĵ������ӣ�����ͬ�Ķ�������ǿ�ų����˶����״�B1���˶���B2������B2��B1����ͼ����ʾ��������ǿ�ų���������Բ���˶������ڡ�tʱ���ڣ��Ÿ�ǿ�ȴ�B1����B2����ͼ����ʾ�����Ÿ�ǿ��ΪB2ʱ���ס��������ӵĶ��ܱ仯Ϊ��������
�ס���������ȫ��ͬ�Ĵ������ӣ�����ͬ�Ķ�������ǿ�ų����˶����״�B1���˶���B2������B2��B1����ͼ����ʾ��������ǿ�ų���������Բ���˶������ڡ�tʱ���ڣ��Ÿ�ǿ�ȴ�B1����B2����ͼ����ʾ�����Ÿ�ǿ��ΪB2ʱ���ס��������ӵĶ��ܱ仯Ϊ��������| A�� | ������ | B�� | �ײ��䣬�Ҽ��� | C�� | �ײ��䣬������ | D�� | ���٣��Ҳ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
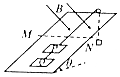 ��ͼ��ʾ���⻬�̶�б�����Ϊ��=37�㣬б������������ȫ��ͬ���������߿�P��Q��ϸ�����ӣ�Pͨ��ƽ����б���ϸ���ƹ�б�涥�˵Ķ�������һ���������ӣ���ʼ����̶����߿��ھ�ֹ��б����ˮƽ����MN�Ϸ��д�ֱ��б�����µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB���߿�ı߳���P�߿����ϱߵ�MN�ľ����ΪL���ͷ����ʹ��������߿���б�������˶��������߿��������Ϊm��ÿ���߿�ĵ����ΪR�����������Ϊ2m�������Ϸ���б���㹻��������������㹻�ߣ��߿��˶������У��ϱ�ʼ����MNƽ�У��������ٶ�Ϊg�����߿�P�պ�Ҫ��ȫ����ų���һ˲�䣬����ļ��ٶ�Ϊ�㣬sin37��=0.6��cos37��=0.8����
��ͼ��ʾ���⻬�̶�б�����Ϊ��=37�㣬б������������ȫ��ͬ���������߿�P��Q��ϸ�����ӣ�Pͨ��ƽ����б���ϸ���ƹ�б�涥�˵Ķ�������һ���������ӣ���ʼ����̶����߿��ھ�ֹ��б����ˮƽ����MN�Ϸ��д�ֱ��б�����µ���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB���߿�ı߳���P�߿����ϱߵ�MN�ľ����ΪL���ͷ����ʹ��������߿���б�������˶��������߿��������Ϊm��ÿ���߿�ĵ����ΪR�����������Ϊ2m�������Ϸ���б���㹻��������������㹻�ߣ��߿��˶������У��ϱ�ʼ����MNƽ�У��������ٶ�Ϊg�����߿�P�պ�Ҫ��ȫ����ų���һ˲�䣬����ļ��ٶ�Ϊ�㣬sin37��=0.6��cos37��=0.8�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
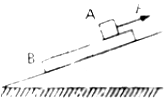 �������A��B�����ڹ⻬��б���ϣ��÷�����б��ƽ�е�����F������A�ϣ�ʹ�����һ����б�������������˶���������˵������ȷ���У�������
�������A��B�����ڹ⻬��б���ϣ��÷�����б��ƽ�е�����F������A�ϣ�ʹ�����һ����б�������������˶���������˵������ȷ���У�������| A�� | ���B�ܵ�A�ľ�Ħ������б������ | B�� | ���B��A�ľ�Ħ������б������ | ||
| C�� | ���A���ܵ��ľ�Ħ������С����F | D�� | ���A���ܵ��ľ�Ħ������СС��F |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com