
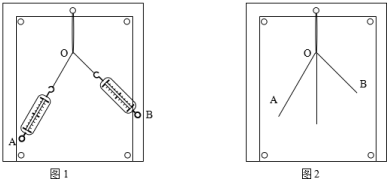
���� ͨ��ͼʾ�����������ɳӵ������Լ�һ�����ɳӵ����������ƽ���ı��ζ��������������ĺ�����ͨ���Ƚϵó�ʵ��Ľ��ۣ�
��� �⣺����ͼʾ������FA��FB��F3�����ƽ���ı��ζ�����������F����ͼ��ʾ����֪����������ķ�Χ�ڣ����ĺϳ���ѭƽ���ı� �ζ���
���
ʵ���в������IJ����Dz��裨3���������¼һ�����ɳ������ķ���
�ʴ�Ϊ����ͼ��ʾ������������ķ�Χ�ڣ����ĺϳ���ѭƽ���ı��ζ����裨3������¼һ�����ɳӵ���������
���� �������Ĺؼ�֪��ʵ��IJ����IJ����Լ�ע�����֪�������ͷ���������Ч����ͬ�����ξ�Ҫ����Ƥ������ͬһ�����0��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | һ����Դ�ĵ綯�ƵĴ�С�����·�й� | |
| B�� | ��綯�Ƶĵ�λ�͵��Ʋ���ͬ�����Ե綯��ʵ���Ͼ��ǵ��Ʋ� | |
| C�� | һ���綯��Ϊ1.5V�ĵ�ؽ����·ʱ������1C�ĵ����ͨ����·������1.5J�Ļ�ѧ��ת��ɵ��� | |
| D�� | �������ѹ���ӵ���Դ����ʱ����ѹ���Ķ�����С���ڵ綯�ƵĴ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�⻬���㹻����б��̶��ڵ����ϣ�б����Ǧ�=30�㣬ƽ����б����ᵯ�ɾ���ϵ��Ϊk=800N/m��һ�˹̶���б��ˣ���һ�������A˩�ӣ����B��б����������A�ϵ���ճ�������A����mA=1.5kg�����B����mB=10.5kg����ʼt0=0ʱ����������ֹ������ƽ����б�����ϵ������������B��ʹB���ȼ����˶�����֪��F��t=0.2s���DZ�������0.2s���Ǻ���������ʼ���ڵ������ڣ��ҵ����α����ȴ�ʱ��������Ҳ�ȴ�gȡ10m/s2����
��ͼ��ʾ��һ�⻬���㹻����б��̶��ڵ����ϣ�б����Ǧ�=30�㣬ƽ����б����ᵯ�ɾ���ϵ��Ϊk=800N/m��һ�˹̶���б��ˣ���һ�������A˩�ӣ����B��б����������A�ϵ���ճ�������A����mA=1.5kg�����B����mB=10.5kg����ʼt0=0ʱ����������ֹ������ƽ����б�����ϵ������������B��ʹB���ȼ����˶�����֪��F��t=0.2s���DZ�������0.2s���Ǻ���������ʼ���ڵ������ڣ��ҵ����α����ȴ�ʱ��������Ҳ�ȴ�gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾΪ���������ˮƽ�̶�����֮�䶯Ħ��������ʵ��װ��ʾ��ͼ��ϸ��ƽ�������棬��֪�����ڹ���������ΪM����������Ϊm���ڹ��Ŀ���Ϊd���������֮��ľ���Ϊs���������ٶ�Ϊg�������ӹ����1������ɾ�ֹ�ͷţ��ֱ����ڹ��ͨ�������1��2���õ�ʱ��t1��t2�����ڹ��ͨ������ŵ�ƽ���ٶȱ�ʾ�ڹ����ֱ����ͨ������ŵ�˲ʱ�ٶȣ�
��ͼ��ʾΪ���������ˮƽ�̶�����֮�䶯Ħ��������ʵ��װ��ʾ��ͼ��ϸ��ƽ�������棬��֪�����ڹ���������ΪM����������Ϊm���ڹ��Ŀ���Ϊd���������֮��ľ���Ϊs���������ٶ�Ϊg�������ӹ����1������ɾ�ֹ�ͷţ��ֱ����ڹ��ͨ�������1��2���õ�ʱ��t1��t2�����ڹ��ͨ������ŵ�ƽ���ٶȱ�ʾ�ڹ����ֱ����ͨ������ŵ�˲ʱ�ٶȣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�������߳���̨H��������̨�ߵľ���ΪL��ij����ƹ����ѵ���У������$\frac{L}{2}$���������ش�ֱ�����ķ���ˮƽ��������ǡ��ͨ�����������䵽�Ҳ�̨���Ե����ƹ�����˶�Ϊƽ���˶�������һ��������������
��ͼ��ʾ�������߳���̨H��������̨�ߵľ���ΪL��ij����ƹ����ѵ���У������$\frac{L}{2}$���������ش�ֱ�����ķ���ˮƽ��������ǡ��ͨ�����������䵽�Ҳ�̨���Ե����ƹ�����˶�Ϊƽ���˶�������һ��������������| A�� | �����ĸ߶������߶�֮��Ϊ2��1 | |
| B�� | ƹ�����������������˶�ʱ��֮��Ϊ2��1 | |
| C�� | ƹ�������ʱ���䵽̨���Եʱ��ֱ��������֮��Ϊ1��2 | |
| D�� | ƹ���������������˶��ٶȱ仯��֮��Ϊ1��2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���Ǵ�С��ȡ������෴���ֱ����������������ϵ��������ض���һ���������ͷ������� | |
| B�� | ���Ǵ�С��ȡ������෴��������ͬһ�����ϵ��������ض���һ���������ͷ������� | |
| C�� | ��ʹ��С��ȡ������෴��������ͬһֱ�����ҷֱ����������������ϵ�������Ҳ��һ����һ���������ͷ������� | |
| D�� | ����õ�һ������������һ�����Ƿ���������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
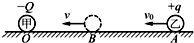 ��ͼ��ʾ��һ�������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ�������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶����˶���B��ʱ�ٶ�Ϊv����Ϊ�˶��������ٶȵ���Сֵ����֪�������ܵ���������С��Ϊf��A��B��������ΪL0������������Ϊk��������˵����ȷ���ǣ�������
��ͼ��ʾ��һ�������Ϊ-Q�ĵ��ɼף��̶��ھ�Եˮƽ���ϵ�O�㣮��һ�������Ϊ+q������Ϊm�ĵ����ң���A���Գ��ٶ�v0�����ǵ���������˶����˶���B��ʱ�ٶ�Ϊv����Ϊ�˶��������ٶȵ���Сֵ����֪�������ܵ���������С��Ϊf��A��B��������ΪL0������������Ϊk��������˵����ȷ���ǣ�������| A�� | �����Ҵ�A������˶��Ĺ����У����ٶ��ȼ�С������ | |
| B�� | �����Ҵ�A������˶��Ĺ����У���������������ټ�С | |
| C�� | O��B�����ľ���Ϊ$\sqrt{\frac{KQq}{f}}$ | |
| D�� | �ڵ��ɼ��γɵĵ糡�У�A��B�����ĵ��Ʋ�ΪUAB=$\frac{f{L}_{0}+\frac{1}{2}m{v}^{2}}{q}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������˶��������е��һ���غ� | |
| B�� | �������˶��������е�ܿ����غ� | |
| C�� | ���������������������㣬��е��һ���غ� | |
| D�� | ����ֻ������ʱ����е�ܲŻ��غ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com