
| A. | 地心是椭圆轨道的一个焦点 | |
| B. | 两火箭一定会在赤道的上空相遇 | |
| C. | 两火箭最远相距L=4($\frac{g{t}^{2}{R}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{2}}$-2R | |
| D. | 火箭距地面的最大高度h=2($\frac{g{t}^{2}{R}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$-R |
分析 从地球南极和北极同时发射的两枚火箭均沿椭圆轨道运行,根据开普勒定律知道地球位于椭圆轨道的一个焦点上.火箭沿近地圆轨道运行时,由地球的万有引力提供向心力,据此列式可得到火箭运行的周期.物体在地球表面上,重力近似等于地球的万有引力,列式可得到重力加速度与地球半径的关系.火箭沿椭圆轨道运行时,由开普勒第三定律列式,得到周期与半长轴a的关系,将几个式子联立求出a,两火箭相距最远l=4a-2R
解答  解:A、从地球南极和北极同时发射的两枚火箭均沿椭圆轨道运行,地球位于椭圆轨道的一个焦点上,则A正确
解:A、从地球南极和北极同时发射的两枚火箭均沿椭圆轨道运行,地球位于椭圆轨道的一个焦点上,则A正确
B、运动轨迹图如图,且二者周期相同,则会在赤道上空相遇.则B正确
C、在椭圆轨道上运行的两枚火箭,当到达最远点时,此时两火箭相距最远.设椭圆轨道的半长轴为a,则两火箭相距最远l=4a-2R.
设火箭沿近地圆轨道运行的周期为T0,火箭由地球的万有引力提供向心力,则得:
G$\frac{Mm}{{R}^{2}}$=m$R\frac{4{π}^{2}}{{T}_{0}^{2}}$ ①
在地面上有:GM=gR2 ②
由①②得:${T}_{0}=\sqrt{\frac{4{π}^{2}R}{g}}$③
设火箭沿椭圆轨道运行的周期为T,根据开普勒第三定律:$\frac{{a}^{3}}{{R}^{3}}=\frac{{T}^{2}}{{T}_{0}^{2}}$④
两火箭最远时,经历了$\frac{T}{2}$=t,即 T=2t⑤
由③④⑤得:$a=\root{3}{\frac{{t}^{2}{R}^{2}g}{{π}^{2}}}$,则L=4a-2R=$4\root{3}{\frac{{t}^{2}{R}^{2}g}{{π}^{2}}}-2R$,则C错误
D、火箭距地面的最大高度h为2l-R=2($\frac{g{t}^{2}{R}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$-R则D正确
故选:ABD
点评 本题关键要理清思路,对于圆周运动,由万有引力等于向心力列式,对椭圆运动,运用开普勒第三定律研究,同时要正确画出火箭的运动轨迹,由几何知识求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:多选题
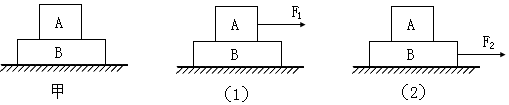
| A. | 在图(1)中,只要F1>3μmg,B就会在地面上滑动 | |
| B. | 在图(1)中,只要F1>4μmg,A就会相对于B滑动 | |
| C. | 在图(2)中,A的加速度最大能达到2μg | |
| D. | 在图(1)和(2)中,当A和B刚要相对滑动时,F1=F2 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
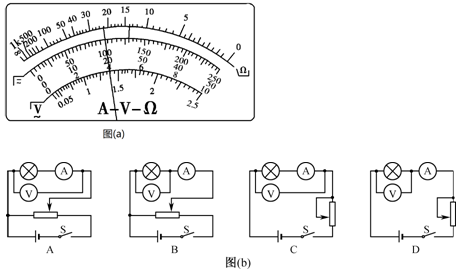
 LED发光二极管具有体积小、亮度高、能耗低、寿命长等诸多优点,已广泛应用于电脑、手机等电子产品中.有一种LED手灯所用发光二极管,它在正常工作时,正向电压约2.8V,电流在10mA左右.现取这样一只发光二极管,要通过测量描绘出它的伏安特性曲线(电压从0到2.8V),提供有下列实验器材:
LED发光二极管具有体积小、亮度高、能耗低、寿命长等诸多优点,已广泛应用于电脑、手机等电子产品中.有一种LED手灯所用发光二极管,它在正常工作时,正向电压约2.8V,电流在10mA左右.现取这样一只发光二极管,要通过测量描绘出它的伏安特性曲线(电压从0到2.8V),提供有下列实验器材:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 若某发电机的正方形线圈以ω=50rad/s的角速度匀速转动,线圈各边长a=40cm,匝数n=100匝,线圈电阻r=1,转动轴OO′穿过线圈对边的中点,整个装置位于磁感应强度B=0.5T的匀强磁场中.线圈为R=9Ω的电阻供电.求:
若某发电机的正方形线圈以ω=50rad/s的角速度匀速转动,线圈各边长a=40cm,匝数n=100匝,线圈电阻r=1,转动轴OO′穿过线圈对边的中点,整个装置位于磁感应强度B=0.5T的匀强磁场中.线圈为R=9Ω的电阻供电.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两个弹性物体只要相互接触就一定会产生弹力 | |
| B. | 静止在水平面上的物体,对水平面的压力就是物体的重力 | |
| C. | 产生弹力的物体一定发生弹性形变 | |
| D. | 微小的力不能使坚硬的物体发生形变 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 在单向直线运动中,位移就是路程 | |
| B. | 平均速度方向一定与位移方向相同 | |
| C. | 速度变化率为0,加速度可能很大 | |
| D. | 速度越来越小,加速度可能越来越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com