
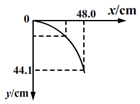
 ����ƽ���˶���ʵ�飺
����ƽ���˶���ʵ�飺���� ��1������ʵ���ԭ��ȷ��������������������Ӷ�ȷ������Ҫ�����ģ�
��2������ʵ���ԭ���Լ�ע������ȷ����ȷ�IJ������裮
��3��������ֱλ�����ƽ���˶���ʱ�䣬���ˮƽλ�ƺ�ʱ��������ٶȣ�
��� �⣺��1��ʵ������Ҫ���ش���ȷ��ľ���Ƿ�����ֱƽ���ڣ��ÿ̶ȳ߲����㼣��ľ��룮����Ҫ����С�������������Ҫ��ƽ��ʱ�����ͨ����ֱλ�����������Ҫ�����
��ѡ��CD��
��2��A��Ϊ�˼�С������Ӱ�죬����ѡ���ܶȴ����С�ģ���A��ȷ��
B��Ϊ�˱�֤С��ij��ٶ�ˮƽ��б��ĩ��������ˮƽ����B��ȷ��
C��Ϊ�˱�֤С��ƽ���˶��ij��ٶ���ͬ��ÿ���ͷ�С���λ������ͬ����C��ȷ��
D��ʵ���������ƽ���������ӣ����������ߣ���D����
��ѡ��ABC��
��3������ֱ�����ϣ�����$y=\frac{1}{2}g{t}^{2}$�ã�t=$\sqrt{\frac{2y}{g}}$=$\sqrt{\frac{2��0.441}{9.8}}s=0.3s$����С��ƽ���˶��ij��ٶ�${v}_{0}=\frac{x}{t}=\frac{0.48}{0.3}m/s=1.6m/s$��
�ʴ�Ϊ����1��CD����2��ABC����3��1.6
���� �������Ĺؼ�֪��ʵ���ԭ���Լ�ע�����֪��ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɣ�����˶�ѧ��ʽ�����⣬�ѶȲ���


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����������0���100���¶��µ�λ���ʼ���ķ�����ռ�ܷ������İٷֱ�������������ʵı仯�ֱ���ͼ������������ʾ������˵����ȷ���ǣ�������
����������0���100���¶��µ�λ���ʼ���ķ�����ռ�ܷ������İٷֱ�������������ʵı仯�ֱ���ͼ������������ʾ������˵����ȷ���ǣ�������| A�� | ͼ�����߶�Ӧ������������ƽ�����ܽ�С������ | |
| B�� | ͼ��ʵ�߶�Ӧ������������100��ʱ������ | |
| C�� | ͼ�����߸����������������������������Ŀ | |
| D�� | ��0��ʱ��ȣ�100��ʱ�����������ʳ�����0��400m/s�����ڵķ�����ռ�ܷ������İٷֱȽϴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��F��F1��Fsin��ʱ�������� | B�� | ��F1=Fsin��ʱ����Ψһ�� | ||
| C�� | ��Fsin�ȣ�F1��Fʱ�������� | D�� | ��F1��Fsin��ʱ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ÿ�����ӵ����� | B�� | ÿ�����ӵ���� | ||
| C�� | ÿ������ռ�ݵĿռ� | D�� | 1g�����������ķ��Ӹ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 С�ͽ���������У����ν����߿�����ǿ�ų�������ת���������ĸ�Ӧ�綯����ʱ������Һ�����ϵ����ͼ��ʾ������Ȧ��һ��R=9���ĵ��蹹�ɱպϵ�·����Ȧ�����ĵ���r=1��������˵����ȷ���ǣ�������
С�ͽ���������У����ν����߿�����ǿ�ų�������ת���������ĸ�Ӧ�綯����ʱ������Һ�����ϵ����ͼ��ʾ������Ȧ��һ��R=9���ĵ��蹹�ɱպϵ�·����Ȧ�����ĵ���r=1��������˵����ȷ���ǣ�������| A�� | �������������Ϊ0.2s | B�� | ���������Ƶ��Ϊ5Hz | ||
| C�� | �������Ӧ�綯�Ƶ����ֵΪ20$\sqrt{2}$V | D�� | ����R�ĵ繦��Ϊ18W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
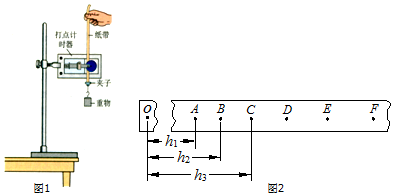
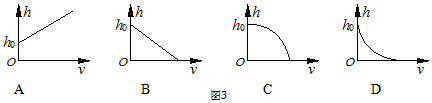
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
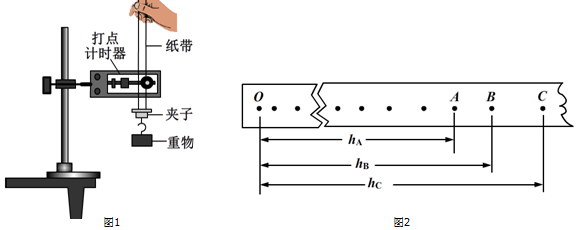
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | $��\frac{{\sqrt{3}}}{2}+1��d$ | B�� | $\frac{{\sqrt{17}}}{2}d$ | C�� | d | D�� | $\frac{{\sqrt{3}}}{2}d$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
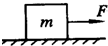 ��ͼ��ʾ������m=10kg���������ˮƽ���ϣ�������ˮƽ��䶯Ħ������Ϊ��=0.4��ȡg=10m/s2�����ô�СΪF=50N��ˮƽ�������������壬ʹ�����ɾ�ֹ��ʼ���ȱ���ֱ���˶�����t=8s����
��ͼ��ʾ������m=10kg���������ˮƽ���ϣ�������ˮƽ��䶯Ħ������Ϊ��=0.4��ȡg=10m/s2�����ô�СΪF=50N��ˮƽ�������������壬ʹ�����ɾ�ֹ��ʼ���ȱ���ֱ���˶�����t=8s�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com