
 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源:不详 题型:计算题
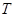 ,地球可看作质量分布均匀的球体,半径为
,地球可看作质量分布均匀的球体,半径为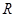 ,表面的重力加速度为
,表面的重力加速度为 。求:
。求: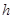 。
。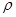 。
。查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| A.月球表面的重力加速度 | B.月球对卫星的吸引力 |
| C.卫星绕月运行的速度 | D.卫星绕月运行的加速度 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
查看答案和解析>>
科目:高中物理 来源:不详 题型:计算题
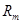 为地球轨道半径
为地球轨道半径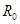 的1.5倍。简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,成为一个绕地球运行的人造卫星;第二步,在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,使探测器沿半个椭圆轨道(该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切)射到火星上。如图(a)所示。已知地球半径
的1.5倍。简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,成为一个绕地球运行的人造卫星;第二步,在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,使探测器沿半个椭圆轨道(该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切)射到火星上。如图(a)所示。已知地球半径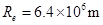 ,重力加速度g=10m/s2。
,重力加速度g=10m/s2。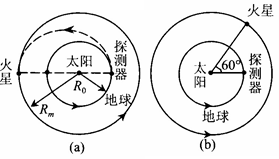
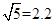 ,1年为365天)。
,1年为365天)。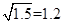 ,1年为365天)。
,1年为365天)。 查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| A.地球绕太阳运行的周期T和地球中心离太阳中心的距离r |
| B.月球绕地球运行的周期T和地球的半径R |
C.月球绕地球运动的角速度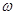 和月球中心离地球中心的距离r 和月球中心离地球中心的距离r |
| D.月球绕地球运动的周期T和轨道半径r |
查看答案和解析>>
科目:高中物理 来源:不详 题型:单选题
| A.月球的半径 | B.月球的质量 |
| C.月球表面的重力加速度 | D.月球绕地球做匀速圆周运动的向心加速度 |
查看答案和解析>>
科目:高中物理 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com