
 “天宫一号”是我国的第一个目标飞行器,于2011年9月29日21时16分在酒泉卫星发射中心发射升空,目前运行在距地面343km的圆轨道上,2012年4月30日4时50分,我国在西昌卫星发射中心成功发射“一箭双星”,将第十二、第十三颗北斗导航系统组网卫星“北斗M”和“北斗-M”顺利送入预定的“中地球”轨道,目前,“北斗M”卫星运行于距地心1.5×4km的圆轨道上,将“天宫一号”和“北斗M”相比,运行速度较大的是天宫一号,运行周期较大的是北斗M.
“天宫一号”是我国的第一个目标飞行器,于2011年9月29日21时16分在酒泉卫星发射中心发射升空,目前运行在距地面343km的圆轨道上,2012年4月30日4时50分,我国在西昌卫星发射中心成功发射“一箭双星”,将第十二、第十三颗北斗导航系统组网卫星“北斗M”和“北斗-M”顺利送入预定的“中地球”轨道,目前,“北斗M”卫星运行于距地心1.5×4km的圆轨道上,将“天宫一号”和“北斗M”相比,运行速度较大的是天宫一号,运行周期较大的是北斗M. 分析 根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}}{{T}^{2}}r$,解出线速度、周期与轨道半径的关系,根据题目中提供的轨道的大小,判断速度和周期的大小.
解答 解:根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,得$v=\sqrt{\frac{GM}{r}}$,轨道越大,速度越小,天宫一号的轨道小于北斗M的轨道,故运行速度较大的是天宫一号;
根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,得$T=2π\sqrt{\frac{{r}^{3}}{GM}}$,由此可知,轨道越大,周期越大,天宫一号的轨道小于北斗M的轨道,故运行周期较大的是北斗M.
故答案为:天宫一号;北斗M.
点评 本题要掌握万有引力提供向心力这个重要的关系,根据题意能够选择恰当的向心力的表达式.


科目:高中物理 来源: 题型:多选题
| A. | 每一种原子都有自己的特征谱线 | |
| B. | 处于n=3的一个氢原子回到基态时可能会辐射三种频率的光子 | |
| C. | α射线的穿透能力比γ射线弱 | |
| D. | β衰变中的电子来自原子的内层电子 | |
| E. | 放射性元素的半衰期与压力、温度无关 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在倾角为θ的光滑斜面上有两个通过轻弹簧连接的物块A和B,C为固定挡板,系统处于静止状态.现开始用变力F沿斜面向上拉动物块A使之做匀加速直线运动,经时间t物块B刚要离开挡板,已知物块的质量均为m,弹簧的劲度系数为k,重力加速度为g.则在此过程中,下列说法正确的是( )
如图所示,在倾角为θ的光滑斜面上有两个通过轻弹簧连接的物块A和B,C为固定挡板,系统处于静止状态.现开始用变力F沿斜面向上拉动物块A使之做匀加速直线运动,经时间t物块B刚要离开挡板,已知物块的质量均为m,弹簧的劲度系数为k,重力加速度为g.则在此过程中,下列说法正确的是( )| A. | 力F的最小值为$\frac{4{m}^{2}gsinθ}{k{t}^{2}}$ | B. | 力F的最大值为$\frac{mgsinθ}{1+\frac{4m}{k{t}^{2}}}$ | ||
| C. | 物块A的位移为$\frac{mgsinθ}{k}$ | D. | 力F做的功为$\frac{2{m}^{2}{g}^{2}si{n}^{2}θ}{k}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
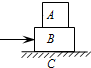 如图所示,C是水平地面,A、B是两个长方形物块,F是作用在物块B上沿水平方向的力,物体A和B以相同的速度作匀加速直线运动.由此可知,A、B间的滑动摩擦系数μ1和B、C间的滑动摩擦系数μ2有可能是( )
如图所示,C是水平地面,A、B是两个长方形物块,F是作用在物块B上沿水平方向的力,物体A和B以相同的速度作匀加速直线运动.由此可知,A、B间的滑动摩擦系数μ1和B、C间的滑动摩擦系数μ2有可能是( )| A. | μ1=0,μ2=0 | B. | μ1=0,μ2≠0 | C. | μ1≠0,μ2=0 | D. | μ1≠0,μ2≠0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,上底为l、下底为3l、高为2l的等腰梯形导线框,以速度v匀速穿过宽为l的磁感应强度为B的匀强磁场时,试作出线框中感应电流随时间变化的i-t图象,线框的电阻为R.(假定逆时针方向的电流为正)
如图所示,上底为l、下底为3l、高为2l的等腰梯形导线框,以速度v匀速穿过宽为l的磁感应强度为B的匀强磁场时,试作出线框中感应电流随时间变化的i-t图象,线框的电阻为R.(假定逆时针方向的电流为正)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
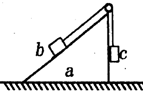 如图所示,斜面体a被放置在水平面上,物块b、c之间用细绳相连,细绳跨过不计摩擦的定滑轮,a、b、c均处于静止状态.若减小c的重力,a、b、c仍保持静止,则( )
如图所示,斜面体a被放置在水平面上,物块b、c之间用细绳相连,细绳跨过不计摩擦的定滑轮,a、b、c均处于静止状态.若减小c的重力,a、b、c仍保持静止,则( )| A. | 水平面对a的摩擦力减小 | B. | 斜面对b的摩擦力减小 | ||
| C. | 斜面对b的支持力减小 | D. | 水平面对a的支持力减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,足够长光滑导轨ab和cd与水平面夹角θ=37°、间距L=0.5m,中间连接一电阻R=2Ω,金属杆PQ与导轨都垂直,并且接触良好,电阻不计,质量m=50g,加上一垂直于斜面的磁场,磁感应强度B=0.5T,将金属杆由静止释放,取重力加速度g=10m/s2,求:
如图所示,足够长光滑导轨ab和cd与水平面夹角θ=37°、间距L=0.5m,中间连接一电阻R=2Ω,金属杆PQ与导轨都垂直,并且接触良好,电阻不计,质量m=50g,加上一垂直于斜面的磁场,磁感应强度B=0.5T,将金属杆由静止释放,取重力加速度g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在界面OO′两侧有两个匀强磁场,磁感应强度分别为B1=1.0T,B2=0.5T,在界面A点处有一带电粒子以初速度v0=15.7m/s垂直界面OO′射入磁场,已知粒子的质量m=2.0×10-9kg,带电荷量q=+3.14×10-7C,
如图所示,在界面OO′两侧有两个匀强磁场,磁感应强度分别为B1=1.0T,B2=0.5T,在界面A点处有一带电粒子以初速度v0=15.7m/s垂直界面OO′射入磁场,已知粒子的质量m=2.0×10-9kg,带电荷量q=+3.14×10-7C,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com