练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    12．一根质量分布不均匀的金属链条重30N，长1m，盘曲在水平地面上，当从链条的A慢慢提起链条到使它的另一端B恰好离开地面需做功12J，如改从B端慢慢提起链条使链条A端恰好离开地面需要做功18J．

    分析 缓慢将提起铁链，需要克服重力做功，根据重力做功公式W=Gh，h是重心上升的高度，求出铁链恰好离开地面时其重心离地面的高度，再确定将B端从地面缓缓上提至A端恰好离开地面重心上升的高度，即可求得需要做功多少．

    解答 解：设将A端从地面缓缓上提至B端恰好离开地面时，铁链的重心离地面的高度为h1，则
       W1=Gh1，得h1=$\frac{{W}_{1}}{G}$=$\frac{12}{30}$m=0.4m
    所以将B端从地面缓缓上提至A端恰好离开地面重心上升的高度为 h2=L-h1=1m-0.4m=0.6m
    需要做功为 W2=Gh2=30×0.6J=18J
    故答案为：18J．

    点评 本题中铁链不能看成质点，求重力做功时，要考虑重心上升的高度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：解答题

    2．某同学要探究一个弹簧秤中的弹簧的劲度系数，实验装置如图1所示，实验中将一透明薄刻度尺（毫米刻度尺）紧贴弹簧秤右边．实验中，读出不挂钩码时弹簧的自然长度，再将钩码逐个加挂在弹簧秤下端（弹簧秤的指针始终指在刻度尺的读数范围内），每次挂完钩码待弹簧秤稳定后测出相应的弹簧总长度．刻度尺不与弹簧秤指针接触，弹簧始终未超过其弹性限度，取g=10m/s2．试分析下列问题：

    （1）根据实验数据，作出了如图2所示的钩码质量m跟弹簧总长度x之间的函数关系图象，由图象求得该弹簧的劲度系数k=28N/m，弹簧的原长x0=6.0cm
    （2）该弹簧秤挂上一个质量为0.028kg的物体后，弹簧的长度为x=0.07m．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    3．在如图所示的电场中的P点放置一正电荷，使其从静止开始运动，其中加速度逐渐增大的是图中的（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

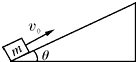    20．如图所示，质量为m=2Kg的木块（可视为质点）沿倾角为θ=53°的足够长的固定斜面以初速度v0=11m/s向上运动，已知木块与斜面间的动摩擦因数为μ=0.5．（g=10/s2）求：
    （1）木块上滑的加速度；
    （2）木块上升的最大位移；
    （3）木块回到斜面原出发点的速度大小．

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

    7．质量为m的汽车，在平直公路上以恒定的加速度匀加速启动，汽车到达额定功率时速度的大小v，此时恰好开始下坡，司机立刻调整发动机的功率为额定功率的一半，使汽车以大小为v的速度沿坡路匀速下滑，下滑一段路程后汽车又开足马力以额定功率加速下滑，在坡路上加速t时间后，车速达到最大，且最大车速是刚下坡时速度的2倍．已知坡面的倾角为θ，重力加速度为g，水平路面和坡面对车的阻力相同，在t时间内汽车沿坡路通过的距离为S．试求：
    （1）汽车的额定功率．
    （2）平直公路和坡面对车的阻力的大小．
    （3）汽车在平直公路上匀加速行驶的加速度的大小．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    17．一个质量为1kg的弹性小球，在光滑水平面上以5m/s的速度垂直撞到墙上，碰撞后小球沿相反方向运动，反弹后的速度大小与碰撞前相同．不及碰撞能量的损失．则碰撞过程中墙对小球做功的大小W为（　　）
    A．W=10JB．W=0JC．W=25JD．W=18J

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    4．下列关于功的说法中正确的是（　　）
    A．由于功有正负，所以功是矢量
    B．计算式W=FScosα中，F是力的大小，S是位移的大小，α是力F和位移S方向上的夹角
    C．合力对物体做的功，等于各分力做功的矢量和
    D．摩擦力做功，一定是负功，起到阻碍作用

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

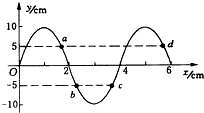    1．如图所示为一列沿x轴传播的简谐横波某时刻的图象．已知从该时刻起，图中质点a比质点b先回到平衡位置，则下列说法中正确的是（　　）
    A．波沿x轴正方向传播
    B．此时刻质点b的速度方向沿y轴正方向
    C．此时刻质点c的速度方向沿y轴正方向
    D．此时刻质点d的加速度方向沿y轴正方向

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    2．太阳系中某行星A运行的轨道半径为R，周期为T，但天文学家在观测中发现，其实际运行的轨道与圆轨道存在一些偏离，且每隔时间t发生一次最大的偏离．形成这种现象的原因可能是A外侧还存在着一颗未知行星B，它对A的万有引力引起A行星轨道的偏离，假设其运动轨道与A在同一平面内，且与A的绕行方向相同，由此可推测未知行星日绕太阳运行的圆轨道半径为（　　）
    A．R$\frac{t}{t-T}$B．R$\root{3}{\frac{tT}{（t-T）^{2}}}$C．R${\root{3}{（\frac{t-T}{t}）^{2}}}^{\;}$D．R$\root{3}{（\frac{t}{t-T}）^{2}}$

    查看答案和解析>>

    同步练习册答案