
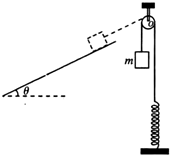
 如图所示,一劲度系数k未知的轻弹簧下端固定于水平地面,上端与不可伸长的轻绳连接,轻绳跨过定滑轮的二端悬挂一个质量为m的重物.用手托住重物,使 得两边轻绳和弹簧都处于竖直状态,轻绳恰能拉直且弹簧处于原长.然后无初速度释 放重物,重物可下落的最大距离为l0不计空气阻力、定滑轮质量及转轴摩擦,重力加速度为g,弹簧的形变在弹性限度内.求
如图所示,一劲度系数k未知的轻弹簧下端固定于水平地面,上端与不可伸长的轻绳连接,轻绳跨过定滑轮的二端悬挂一个质量为m的重物.用手托住重物,使 得两边轻绳和弹簧都处于竖直状态,轻绳恰能拉直且弹簧处于原长.然后无初速度释 放重物,重物可下落的最大距离为l0不计空气阻力、定滑轮质量及转轴摩擦,重力加速度为g,弹簧的形变在弹性限度内.求分析 (1)重物与弹簧组成的系统机械能守恒,由机械能守恒定律可以求出最大弹性势能.
(2)由能量守恒定律可以求出初速度.
(3)根据动摩擦因数大小与斜面倾角的关系,应用平衡条件、弹性势能表达式求出弹性势能.
解答 解:(1)、重物下落l过程它与弹簧组成的系统机械能守恒,
由机械能守恒定律得,弹簧的最大弹性势能:EPmax=mgl;
(2)、由(1)可知,重物在斜面上下滑l距离时,弹簧的弹性势能最大,
最大弹性势能:EPmax′=EPmax=mgl,
由能量守恒定律得:$\frac{1}{2}$mv02+mglsinθ=μmglcosθ+EPmax′,
解得:v0=$\sqrt{2gl(1+μcosθ-sinθ)}$;
(3)若μ≥tanθ,则重物在斜面上获得的初速度v0是其最大速度,所求弹性势能为零;
若μ<tanθ,在(2)的情况下,重物可能在斜面上做往复运动,当第一次到达平衡位置时,
摩擦损失的能量最少,速度最大,设此时弹簧的伸长量为x,弹簧的劲度系数为k,绳子拉力为T,
有:T=kx,mgsinθ=T+μmgcosθ,
在(2)的情况下,弹簧在原长与最大伸长量之间振动,由对称性可知,
其平衡位置在伸长量为$\frac{1}{2}$l处,有:mg=$\frac{1}{2}$kl,
由题意可知,所求弹性势能:Ex=$\frac{1}{2}$kx2,解得:Ex=$\frac{1}{4}$mgl(sinθ-μcosθ)2;
答:(1)重物下落过程,弹簧的最大弹性势能是mgl;
(2)给重物沿斜面向下的初速度至少为v$\sqrt{2gl(1+μcosθ-sinθ)}$;
(3)若μ≥tanθ,弹簧的弹性势能Ex是0;若μ<tanθ,弹簧的弹性势能Ex是$\frac{1}{4}$mgl(sinθ-μcosθ)2.
点评 本题考查了求弹性势能、初速度问题,分析清楚物体运动过程,应用机械能守恒定律、平衡条件、能量守恒定律即可正确解题,此题难度较大.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中物理 来源: 题型:解答题
| 启动的快慢/s (0-30ms的加速时间) | 最大速度m•s-1 | |
| 甲车 | 12 | 40 |
| 乙 | 6 | 50 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,直角三角形ABC为一棱镜的截面,∠A=30°,AC边长为a,一束光以45°的入射角从AC边的中点M射入棱镜,并垂直AB边由N点射出,则棱镜材料的折射率为$\sqrt{2}$;已知光在真空中的速度为c,则这束光在棱镜中传播的时间为$\frac{\sqrt{2}a}{4c}$.
如图所示,直角三角形ABC为一棱镜的截面,∠A=30°,AC边长为a,一束光以45°的入射角从AC边的中点M射入棱镜,并垂直AB边由N点射出,则棱镜材料的折射率为$\sqrt{2}$;已知光在真空中的速度为c,则这束光在棱镜中传播的时间为$\frac{\sqrt{2}a}{4c}$.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 它们的运行速度都小于7.9km/s | |
| B. | 它们运行周期的大小可能不同 | |
| C. | 它们离地心的距离可能不同 | |
| D. | 它们的向心加速度小于静止在赤道上物体的向心加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 伽利略用“理想实验”推翻了亚里斯多德的“力是维持物体运动的原因”的观点 | |
| B. | 从牛顿第一定律可演绎出“质量是物体惯性大小的量度”的结论 | |
| C. | 库仑最早引入电场概念并提出用电场线表示电场 | |
| D. | T•m2与V•s能表示同一个物理量的单位 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
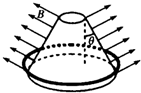 如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B,圆台母线与竖直方向的夹角为θ.一个质量为m、半径为r的匀质金属圆环位于圆台底部.圆环中维持恒定的电流I,圆环由静止向上运动,经过时间t后撤去该恒定电流并保持圆环闭合,圆环上升的最大高度为H.已知重力加速度为g,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是( )
如图所示,空间存在着与圆台母线垂直向外的磁场,各处的磁感应强度大小均为B,圆台母线与竖直方向的夹角为θ.一个质量为m、半径为r的匀质金属圆环位于圆台底部.圆环中维持恒定的电流I,圆环由静止向上运动,经过时间t后撤去该恒定电流并保持圆环闭合,圆环上升的最大高度为H.已知重力加速度为g,磁场的范围足够大.在圆环向上运动的过程中,下列说法正确的是( )| A. | 安培力对圆环做的功为mgH | |
| B. | 圆环先做匀加速运动后做匀减速运动 | |
| C. | 圆环运动的最大速度为$\frac{2πBIrtcosθ}{m}$-gt | |
| D. | 圆环先有扩张后有收缩的趋势 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com