
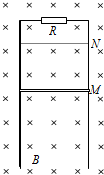
 如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.
如图所示,在磁感应强度为B的水平匀强磁场中,有一竖直放置的光滑的平行金属导轨,导轨平面与磁场垂直,导轨间距为L,顶端接有阻值为R的电阻.将一根金属棒从导轨上的M处以速度v0竖直向上抛出,棒到达N处后返回,回到出发点M时棒的速度为抛出时的一半.已知棒的长度为L,质量为m,电阻为r.金属棒始终在磁场中运动,处于水平且与导轨接触良好,忽略导轨的电阻.重力加速度为g.分析 (1)金属棒从M点被抛出至落回M点的整个过程中,动能减少转化为电能,根据能量守恒定律求电阻R消耗的电能.由于金属棒在运动过程中所受的安培力随着速度的变化而变化,做的是非匀变速运动,不能用运动学公式求时间,可运用动量定理和微元法结合求解.
(2)当金属棒向下运动达到稳定状态时重力的功率等于回路的电功率.根据电流的微观表达式I=neSv和金属棒生热功率公式Pr=(nSL)fv,结合进行解答.
解答 解:
(1)a.金属棒从M点被抛出至落回M点的整个过程中,由能量守恒
回路中消耗的电能 $Q=\frac{1}{2}mv_0^2-\frac{1}{2}m{({\frac{v_0}{2}})^2}=\frac{3}{8}mv_0^2$
电阻R消耗的电能 ${Q_R}=\frac{R}{R+r}•Q=\frac{3Rmv_0^2}{8(R+r)}$
b.方法一:
金属棒从M点被抛出至落回M点的整个过程中,取向下为正方向,由动量定理得:$mg•t+{I_安}=m•\frac{v_0}{2}-({-m{v_0}})$
将整个运动过程划分成很多小段,可认为在每个小段中感应电动势几乎不变,设每小段的时间为△t.
则安培力的冲量 I安=Bi1L•△t+Bi2L•△t+Bi3L•△t+…I安=BL(i1•△t+i2•△t+i3•△t+…)I安=BLq
又 $q=\overline It$,
$\overline I=\frac{\overline E}{R+r}$,
$\overline E=\frac{△Φ}{t}$
因为△Φ=0,
所以I安=0
解得 $t=\frac{{3{v_0}}}{2g}$
方法二:
金属棒从M点被抛出至落回M点的整个过程中,由动量定理$mg•t+{I_安}=m•\frac{v_0}{2}-({-m{v_0}})$
将整个运动过程划分成很多小段,可认为在每个小段中感应电动势几乎不变,设每小段的时间为△t.
则安培力的冲量${I_安}=\frac{{{B^2}{L^2}}}{R+r}{v_1}•△t+\frac{{{B^2}{L^2}}}{R+r}{v_2}•△t+\frac{{{B^2}{L^2}}}{R+r}{v_3}•△t+…$${I_安}=\frac{{{B^2}{L^2}}}{R+r}({v_1}•△t+{v_2}•△t+{v_3}•△t+…)$
因为棒的位移为0,则 v1•△t+v2•△t+v3•△t+…=0
所以 I安=0
解得 $t=\frac{{3{v_0}}}{2g}$
方法三:
金属棒从M点被抛出至落回M点的整个过程中,由动量定理得 $mg•t+{I_安}=m•\frac{v_0}{2}-({-m{v_0}})$
棒的速度v随时间t变化的图象如图所示.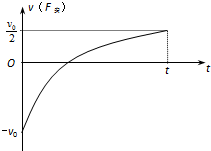
因为棒所受安培力${F_安}=BiL=\frac{{{B^2}{L^2}}}{R+r}•v∝v$
所以棒所受安培力F安随时间t变化的图象亦大致如此.
棒的位移为0,则v-t图线与横轴所围“总面积”为0,F安-t图线与横轴所围“总面积”也为0,即整个过程中安培力的冲量I安=0.
解得 $t=\frac{{3{v_0}}}{2g}$
(2)方法一:
当金属棒向下运动达到稳定状态时 mg=Fm
其中 ${F_m}=\frac{{{B^2}{L^2}{v_m}}}{R+r}$
解得 ${v_m}=\frac{{mg({R+r})}}{{{B^2}{L^2}}}$
沿棒方向,棒中自由电子受到洛伦兹力evmB、电场力eE和金属离子对它的平均作用力f作用.因为棒中电流恒定,所以自由电子沿棒的运动可视为匀速运动.
则 f+eE=evmB
又 $E=\frac{U}{L}$$U=\frac{{BL{v_m}}}{R+r}•R$
解得 $f=\frac{emgr}{{B{L^2}}}$
方法二:
当金属棒向下运动达到稳定状态时
单位时间内机械能减少 P=mgvm
金属棒生热功率 Pr=$\frac{r}{R+r}P$
回路中的电流 $I=\frac{{BL{v_m}}}{R+r}$
设棒的横截面积为S,棒中单位体积内的自由电子数为n,棒中自由电子定向移动的速度为v,金属离子对自由电子的平均作用力为f.
则 Pr=(nSL)fv,I=neSv.
所以 $f=\frac{emgr}{{B{L^2}}}$
答:
(1)金属棒从M点被抛出至落回M点的整个过程中,a.电阻R消耗的电能为$\frac{3Rm{v}_{0}^{2}}{8(R+r)}$;b.金属棒运动的时间为$\frac{3{v}_{0}}{2g}$.
(2)当金属棒向下运动达到稳定状态时,棒中金属离子对一个自由电子沿棒方向的平均作用力大小为$\frac{emgr}{B{L}^{2}}$.
点评 解决本题的关键是学会运用微元法求变加速运动的时间,掌握金属棒稳定的条件,理解宏观与微观联系的桥梁是电流的微观表达式.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中物理 来源: 题型:解答题
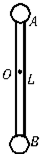 一根轻杆长L,两端各固定一个质量为m的小球A和B,在距A球$\frac{L}{3}$处有一转轴O,当杆绕轴在竖直平面内匀速转动时,周期T=2π$\sqrt{\frac{L}{g}}$,当杆转到如图所示的竖直位置时,求两球对杆的作用力.
一根轻杆长L,两端各固定一个质量为m的小球A和B,在距A球$\frac{L}{3}$处有一转轴O,当杆绕轴在竖直平面内匀速转动时,周期T=2π$\sqrt{\frac{L}{g}}$,当杆转到如图所示的竖直位置时,求两球对杆的作用力.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,为一个均匀透明介质球,球心位于O点,半径为R.一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}R}{2}$.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )
如图所示,为一个均匀透明介质球,球心位于O点,半径为R.一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H=$\frac{\sqrt{3}R}{2}$.若该光束射入球体经一次反射后由E点(图中未标出)再次折射回真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c,则( )| A. | 介质球的折射率为n=3 | |
| B. | 若增大入射光的频率,则该出射光线仍与入射光线平行 | |
| C. | 光束从C点射入到从E点射出所经历的总时间为$\frac{6R}{C}$ | |
| D. | 若介质球的折射率增大,则该出射光线仍与入射光线平行 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

 改装成量程为3V的电压表.该电流计
改装成量程为3V的电压表.该电流计 内部由表头和定值电阻r串联组成,其中表头电阻rg=100Ω,r约为几千欧.为确定该电流计
内部由表头和定值电阻r串联组成,其中表头电阻rg=100Ω,r约为几千欧.为确定该电流计 的满偏电流Ig和r的阻值,他采用如图2所示电路进行测量.
的满偏电流Ig和r的阻值,他采用如图2所示电路进行测量. 满偏,记录此时电阻箱接入电路的阻值R和电压表的示数U;
满偏,记录此时电阻箱接入电路的阻值R和电压表的示数U; 串联(选填“串”或“并”)一个阻值为7.5kΩ的电阻,就可以将该电流计
串联(选填“串”或“并”)一个阻值为7.5kΩ的电阻,就可以将该电流计 改装成量程为3V的电压表.
改装成量程为3V的电压表.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示为游乐场中过山车的一段轨道,P点是这段轨道的最高点,A、B、C三处是过山车的车头、中点和车尾.假设这段轨道是圆轨道,各节车厢的质量相等,过山车在运行过程中不受牵引力,所受阻力可忽略.那么,过山车在通过P点的过程中,下列说法正确的是( )
如图所示为游乐场中过山车的一段轨道,P点是这段轨道的最高点,A、B、C三处是过山车的车头、中点和车尾.假设这段轨道是圆轨道,各节车厢的质量相等,过山车在运行过程中不受牵引力,所受阻力可忽略.那么,过山车在通过P点的过程中,下列说法正确的是( )| A. | 车头A通过P点时的速度最小 | B. | 车的中点B通过P点时的速度最小 | ||
| C. | 车尾C通过P点时的速度最小 | D. | A、B、C通过P点时的速度一样大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 一定质量的理想气体,在等压膨胀过程中,气体分子的平均动能增大 | |
| B. | 若两分子间距离减小,分子间斥力增大、引力减小,合力为斥力 | |
| C. | 在围绕地球运行的“天宫一号”内,飘浮的水滴呈球形,这是表面张力作用的结果 | |
| D. | 布朗运动是由于液体各部分的温度不同而引起的 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m2的木板静止在光滑水平面上,在木板上放一个m1的木块.现给木块一个相对地面的水平速度v0.已知木块与木板间动摩擦因数$μ,\\;\\;\\;\\;因此\\;\\;木板\\;\\;\\;\\;\\;\\;\\;\\;木块$因此木板被木块带动,最后木板与木块以共同的速度运动.求此过程中木块在木板上滑行的距离.
如图所示,质量为m2的木板静止在光滑水平面上,在木板上放一个m1的木块.现给木块一个相对地面的水平速度v0.已知木块与木板间动摩擦因数$μ,\\;\\;\\;\\;因此\\;\\;木板\\;\\;\\;\\;\\;\\;\\;\\;木块$因此木板被木块带动,最后木板与木块以共同的速度运动.求此过程中木块在木板上滑行的距离.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2 | B. | 239 | C. | 145 | D. | 92 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| U(V) | 0 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 1.00 | 1.20 |
| I(A) | 0 | 0.20 | 0.0 | 0.40 | 0.55 | 0.75 | 1.25 | 1.80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com