
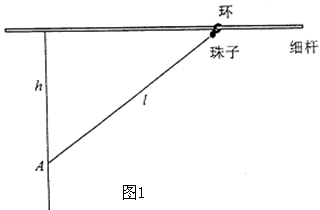
(26分)一根不可伸长的细轻绳,穿上一粒质量为![]() 的珠子(视为质点),绳的下端固定在
的珠子(视为质点),绳的下端固定在![]() 点,上端系在轻质小环上,小环可沿固定的水平细杆滑动(小环的质量及与细杆摩擦皆可忽略不计),细杆与
点,上端系在轻质小环上,小环可沿固定的水平细杆滑动(小环的质量及与细杆摩擦皆可忽略不计),细杆与![]() 在同一竖直平面内.开始时,珠子紧靠小环,绳被拉直,如图1所示,已知,绳长为
在同一竖直平面内.开始时,珠子紧靠小环,绳被拉直,如图1所示,已知,绳长为![]() ,
,![]() 点到杆的距离为
点到杆的距离为![]() ,绳能承受的最大张力为
,绳能承受的最大张力为![]() ,珠子下滑过程中到达最低点前绳子被拉断,求细绳被拉断时珠子的位置和速度的大小(珠子与绳子之间无摩擦)
,珠子下滑过程中到达最低点前绳子被拉断,求细绳被拉断时珠子的位置和速度的大小(珠子与绳子之间无摩擦)
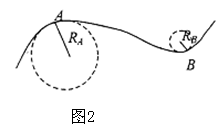
注:质点在平面内做曲线运动时,它在任一点的加速度沿该点轨道法线方向的分量称为法向加速度![]() ,可以证明,
,可以证明,![]() ,
,![]() 为质点在该点时速度的大小,
为质点在该点时速度的大小,![]() 为轨道曲线在该点的“曲率半径”,所谓平面曲线上某点的曲率半径,就是在曲线上取包含该点在内的一段弧,当这段弧极小时,可以把它看做是某个“圆”的弧,则此圆的半径就是曲线在该点的曲率半径.如图2中曲线在
为轨道曲线在该点的“曲率半径”,所谓平面曲线上某点的曲率半径,就是在曲线上取包含该点在内的一段弧,当这段弧极小时,可以把它看做是某个“圆”的弧,则此圆的半径就是曲线在该点的曲率半径.如图2中曲线在![]() 点的曲率半径为
点的曲率半径为![]() ,在
,在![]() 点的曲率半径为
点的曲率半径为![]() .
.
解析:
1. 珠子运动的轨迹
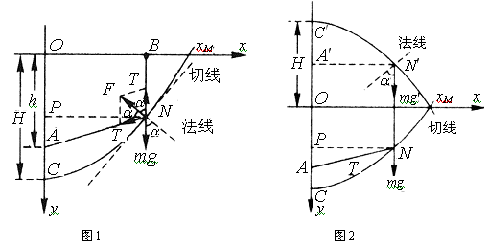
建立如图1所示的坐标系,原点![]() 在过
在过![]() 点的竖直线与细杆相交处,
点的竖直线与细杆相交处,![]() 轴沿细杆向右,
轴沿细杆向右,![]() 轴沿
轴沿![]() 向下。当珠子运动到
向下。当珠子运动到![]() 点处且绳子未断时,小环在
点处且绳子未断时,小环在![]() 处,
处,![]() 垂直于
垂直于![]() 轴,所以珠子的坐标为
轴,所以珠子的坐标为
![]()
由![]() 知
知
![]()
即有![]() ,得
,得
![]() (1)
(1)
这是一个以![]() 轴为对称轴,顶点位于
轴为对称轴,顶点位于![]() 处,焦点与顶点的距离为
处,焦点与顶点的距离为![]() 的抛物线,如图2所示,图中的
的抛物线,如图2所示,图中的![]() ,
,![]() 为焦点。
为焦点。
2. 珠子在![]() 点的运动方程
点的运动方程
因为忽略绳子的质量,所以可把与珠子接触的那一小段绳子看做是珠子的一部分,则珠子受的力有三个,一是重力![]() ;另外两个是两绳子对珠子的拉力,它们分别沿
;另外两个是两绳子对珠子的拉力,它们分别沿![]() 和
和![]() 方向,这两个拉力大小相等,皆用
方向,这两个拉力大小相等,皆用![]() 表示,则它们的合力的大小为
表示,则它们的合力的大小为
![]() (2)
(2)
![]() 为
为![]() 点两边绳子之间夹角的一半,
点两边绳子之间夹角的一半,![]() 沿
沿![]() 的角平分线方向。
的角平分线方向。
因为![]() 是焦点至
是焦点至![]() 的连线,
的连线,![]() 平行于
平行于![]() 轴,根据解析几何所述的抛物线性质可知,
轴,根据解析几何所述的抛物线性质可知,![]() 点的法线是
点的法线是![]() 的角平分线.故合力
的角平分线.故合力![]() 的方向与
的方向与![]() 点的法线一致。
点的法线一致。
由以上的论证.再根据牛顿定律和题中的注,珠子在![]() 点的运动方程(沿法线方向)应为
点的运动方程(沿法线方向)应为
![]() (3)
(3)
![]() (4)
(4)
式中![]() 是
是![]() 点处轨道曲线的曲率半径;
点处轨道曲线的曲率半径;![]() 为珠子在
为珠子在![]() 处时速度的大小。根据机械能守恒定律可得
处时速度的大小。根据机械能守恒定律可得
![]() (5)
(5)
3. 求曲车半径![]()
当绳子断裂时![]() ,由(4)式可见,如果我们能另想其他办法求得曲率半径
,由(4)式可见,如果我们能另想其他办法求得曲率半径![]() 与
与![]() 的关系,则就可能由(4)、(5)两式求得绳子断裂时珠子的纵坐标
的关系,则就可能由(4)、(5)两式求得绳子断裂时珠子的纵坐标![]() 。现提出如下一种办法。做一条与小珠轨迹对于
。现提出如下一种办法。做一条与小珠轨迹对于![]() 轴呈对称状态的抛物线,如图复解19-7-2所示。由此很容易想到这是一个从高
轴呈对称状态的抛物线,如图复解19-7-2所示。由此很容易想到这是一个从高![]() 处平抛物体的轨迹。平抛运动是我们熟悉的,我们不仅知道其轨迹是抛物线,而且知道其受力情况及详细的运动学方程。这样我们可不必通过轨道方程而是运用力学原理分析其运动过程即可求出与
处平抛物体的轨迹。平抛运动是我们熟悉的,我们不仅知道其轨迹是抛物线,而且知道其受力情况及详细的运动学方程。这样我们可不必通过轨道方程而是运用力学原理分析其运动过程即可求出与![]() 对称的
对称的![]() 点处抛物线的曲率半径
点处抛物线的曲率半径![]() 与
与![]() 的关系,也就是
的关系,也就是![]() 处抛物线的曲率半径
处抛物线的曲率半径![]() 与
与![]() 的关系。
的关系。
设从抛出至落地的时间为![]() ,则有
,则有
![]()
由此解得
![]() (7)
(7)
设物体在![]() 处的速度为
处的速度为![]() ,由机械能守恒定律可得
,由机械能守恒定律可得
![]() (8)
(8)
物体在![]() 处法线方向的运动方程为
处法线方向的运动方程为
![]() (9)
(9)
式中![]() 即为
即为![]() 处抛物线的曲率半径,从(7)、(8)、(9)式及
处抛物线的曲率半径,从(7)、(8)、(9)式及![]() ,可求得
,可求得
![]()
这也等于![]() 点抛物线的曲率半径,
点抛物线的曲率半径,![]() ,故得
,故得
![]() (10)
(10)
4. 求绳被拉断时小珠的位置和速度的大小
把(5)式和(10)式代入(4)式,可求得绳子的张力为
![]() (11)
(11)
当![]() 时绳子被拉断,设此时珠子位置的坐标为
时绳子被拉断,设此时珠子位置的坐标为![]() ,由(11)式得
,由(11)式得
![]() (12)
(12)
代入(1)式,得
![]() (13)
(13)
绳子断开时珠子速度的大小为
![]() (14)
(14)


科目:高中物理 来源: 题型:
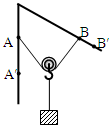 (2013?徐汇区一模)如图所示,一根不可伸长的细绳两端分别连接在固定框架上的A、B两点,细绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,处于静止状态.若缓慢移动细绳的端点,则绳中拉力大小的变化情况是( )
(2013?徐汇区一模)如图所示,一根不可伸长的细绳两端分别连接在固定框架上的A、B两点,细绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,处于静止状态.若缓慢移动细绳的端点,则绳中拉力大小的变化情况是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量为M的长板静置在光滑的水平面上,左侧固定一劲度系数为K且足够长的水平轻质弹簧,右侧用一根不可伸长的细绳连接于墙上(细绳张紧),细绳所能承受的最大拉力为T.让一质量为m、初速为v0的小滑块在长板上无摩擦地对准弹簧水平向左运动.试求:
如图所示,质量为M的长板静置在光滑的水平面上,左侧固定一劲度系数为K且足够长的水平轻质弹簧,右侧用一根不可伸长的细绳连接于墙上(细绳张紧),细绳所能承受的最大拉力为T.让一质量为m、初速为v0的小滑块在长板上无摩擦地对准弹簧水平向左运动.试求:查看答案和解析>>
科目:高中物理 来源: 题型:
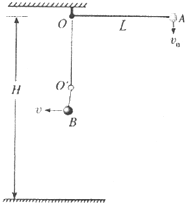 在离地面高H=2L的O点,固定一根长为L不可伸长的细轻绳,绳端系一质量为m、带电量为+q的小球,整个空间存在竖直向下的匀强电场(图中未画出),电场强度E=
在离地面高H=2L的O点,固定一根长为L不可伸长的细轻绳,绳端系一质量为m、带电量为+q的小球,整个空间存在竖直向下的匀强电场(图中未画出),电场强度E=| mg |
| q |
| 3L |
| 4 |
查看答案和解析>>
科目:高中物理 来源:2012-2013学年上海市徐汇区高三上学期期末考试物理试卷(解析版) 题型:选择题
如图所示,一根不可伸长的细绳两端分别连接在固定框架上的A、B两点,细绳绕过光滑的轻小滑轮,重物悬挂于滑轮下,处于静止状态.若缓慢移动细绳的端点,则绳中拉力大小的变化情况是( )

A.只将绳的左端移向A′点,拉力变小
B.只将绳的左端移向A′点,拉力不变
C.只将绳的右端移向B′点,拉力变小
D.只将绳的右端移向B′点,拉力不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com