
 如图所示的装置,水平传送带PQ间距L1=3m,传送带匀速运动的速度v0=1m/s,倾角θ=37°斜面底端固定一轻弹簧,轻弹簧处于原厂时上端位于C点,Q点与斜面平滑连接,Q到C点的距离L2=0.75m,质量m=5kg的物体(科士威质点)无初速度轻纺在传送带左端的P点,当舞台被传送到右端Q点后沿斜面向下滑动,将弹簧压缩到最短位置D点后恰能弹回C点.不计物体经过Q点时机械能的损失,物体与传送带、斜面间的动摩擦因数为μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8).求:
如图所示的装置,水平传送带PQ间距L1=3m,传送带匀速运动的速度v0=1m/s,倾角θ=37°斜面底端固定一轻弹簧,轻弹簧处于原厂时上端位于C点,Q点与斜面平滑连接,Q到C点的距离L2=0.75m,质量m=5kg的物体(科士威质点)无初速度轻纺在传送带左端的P点,当舞台被传送到右端Q点后沿斜面向下滑动,将弹簧压缩到最短位置D点后恰能弹回C点.不计物体经过Q点时机械能的损失,物体与传送带、斜面间的动摩擦因数为μ=0.5(g取10m/s2,sin37°=0.6,cos37°=0.8).求:分析 (1)物体在传送带上先加速后匀速,利用牛顿第二定律和运动学公式求的时间;
(2物体在下面下滑到C的整个过程中利用动能定理求的物体通过的位移,即可判断弹簧的最大压缩量,从压缩到最大到恢复到C点由动能定理可得弹簧的弹性势能;
(3)根据动能定理利用数学知识即可判断速度最大的位置
解答 解:(1)物体在传送带上产生的加速度为:a=$\frac{μmg}{m}=5m/{s}^{2}$
达到和传送带具有相同速度所需时间为:t1=$\frac{{v}_{0}}{a}=\frac{1}{5}s=0.2s$
在0.2s内前进的位移为:x=$\frac{1}{2}a{t}^{2}=\frac{1}{2}×5×0.{2}^{2}m=0.1m$
之后匀速运动,匀速运动时间为:${t}_{2}=\frac{{L}_{1}-x}{v}=\frac{3-0.1}{1}s=2.9s$
到达Q点时间为:t=t1+t2=3s
(2)从Q点到C点的整个过程中由动能定理可得:
$mg{L}_{2}sinθ-μmgxcosθ=0-\frac{1}{2}{mv}_{0}^{2}$
解得:x=1m
故弹簧的压缩量为:$x′=\frac{1-0.75}{2}m=0.125m$
从压缩到最大到恢复到C点由动能定理可得:
EP-μmgx′cosθ-mgx′sinθ=0-0
解得:EP=6.25J
(3)根据动能定理可得:
${E}_{P}-μmgx′cosθ-mgx′sinθ=\frac{1}{2}m{v}^{2}$
v=$\sqrt{kx{′}^{2}-2μgx′cosθ-2gx′sinθ}$
当且仅当x$′=\frac{10}{k}$时速度最大
答:(1)物体从p点运动到Q点的时间为3s;
(2)物体压缩弹簧过程中弹簧的最大弹性势能为6.25J;
(3)若已知弹簧的弹性势能与弹簧的劲度系数k和形变量的关系式Ep=$\frac{1}{2}$kx2,物体被弹簧弹回$\frac{10}{k}$时速度最
点评 本题主要考查了动能定理,在传送带上物体先加速后匀速,在斜面上利用动能定理求的物体通过的总位移,即可求得弹簧的压缩量即可


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,汽车在一段弯曲水平路面上匀速行驶,关于它受到的水平方向的作用力方向的示意图,可能正确的是(图中F为地面对它的静摩擦力,f为它行驶时所受的阻力)( )
如图所示,汽车在一段弯曲水平路面上匀速行驶,关于它受到的水平方向的作用力方向的示意图,可能正确的是(图中F为地面对它的静摩擦力,f为它行驶时所受的阻力)( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 飞机做特技表演时常做俯冲拉起运动.如图所示.此运动在最低点附近可看作是半径为1000m的圆周运动.若飞行员的质量为68kg,飞机经过最低点时的速度为360km/h.(重力加速度取g=10m/s2).则
飞机做特技表演时常做俯冲拉起运动.如图所示.此运动在最低点附近可看作是半径为1000m的圆周运动.若飞行员的质量为68kg,飞机经过最低点时的速度为360km/h.(重力加速度取g=10m/s2).则查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
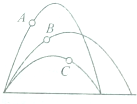 以相同的初速率、不同的抛射角同时抛出三个小球A、B、C,在空中的运动轨迹如图所示,则下列说法中错误的是( )
以相同的初速率、不同的抛射角同时抛出三个小球A、B、C,在空中的运动轨迹如图所示,则下列说法中错误的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以落地最迟 | |
| C. | A球的射高最大,所以落地最迟 | |
| D. | A、C两球的射程相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 利用激光束的反射,用s=c•$\frac{t}{2}$计算出s | |
| B. | 利用月球运动的线速度及周期关系v=$\frac{2π(s+R+r)}{T}$计算s | |
| C. | 利用地球表面的重力加速度、地球半径及月球运动的线速度关系m月g0=m月$\frac{v^2}{s+R+r}$计算s | |
| D. | 利用月球表面的重力加速度、地球半径及月球运动周期关系m月g′=m月$\frac{{4{π^2}}}{T^2}$(s+R+r)计算s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com