
 天文学家经过长期观察,在河外星系发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.A、B围绕两者连线上的O点作匀速圆周运动,它们之间的距离r保持不变,如图所示.已知A、B两星的质量分别为m、M,且可视为质点,不考虑其它天体的影响,万有引力常量为G,则下列说法中正确的是( )
天文学家经过长期观察,在河外星系发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.A、B围绕两者连线上的O点作匀速圆周运动,它们之间的距离r保持不变,如图所示.已知A、B两星的质量分别为m、M,且可视为质点,不考虑其它天体的影响,万有引力常量为G,则下列说法中正确的是( )| A. | 两星运动的角速度之比ωA:ωB=m:M | |
| B. | 两星运动的线速度之比vA:vB=(m+M):M | |
| C. | 两星运动的向心加速度之比aA:aB=M:m | |
| D. | A星运动周期T=2$π\sqrt{\frac{{r}^{2}}{G(m+M)}}$ |
分析 抓住A、B做圆周运动的向心力相等,角速度相等,求出A、B轨道半径的关系,从而得知A、B距离为A卫星的轨道半径关系,由v=ωr求出线速度的关系.
根据牛顿第二定律得出加速度的大小关系;
根据万有引力提供向心力求出A的周期.
解答 解:A、A、B围绕两者连线上的O点作匀速圆周运动,它们的角速度是相等的.故A错误;
B、设A、B圆轨道的半径分别为r1、r2,由题意知,A、B的角速度相等,为ω,
有:${F}_{A}=m{r}_{1}{ω}^{2}$,${F}_{B}=M{r}_{2}{ω}^{2}$,又FA=FB.
所以:$\frac{{r}_{1}}{{r}_{2}}=\frac{M}{m}$
又:v=ωr
所以:$\frac{{v}_{A}}{{v}_{B}}=\frac{{r}_{1}}{{r}_{2}}=\frac{M}{m}$.故B错误;
C、二者之间的万有引力大小相等,方向相反,根据牛顿第二定律:F=ma可得:
$\frac{{a}_{A}}{{a}_{B}}=\frac{M}{m}$.故C正确;
D、A、B之间的距离为r,由万有引力定律得,${F}_{A}=\frac{GmM}{{r}^{2}}$=$\frac{m•4{π}^{2}r}{{T}^{2}}$.
联立得:T=$2π\sqrt{\frac{{r}^{3}}{GM}}$.故D错误.
故选:C
点评 本题是双子星问题,关键抓住双子星所受的万有引力相等,转动的角速度相等,根据万有引力定律和牛顿第二定律综合求解.


科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 北京时间2016年10月19日凌晨“神舟十一号”载人飞船与“天宫二号”成功进行对接.在对接前,“神舟十一号”的运行轨道高度为341km,“天宫二号”的运行轨道高度为393km,它们在各自轨道上作匀速圆周运动时,下列判断正确的是( )
北京时间2016年10月19日凌晨“神舟十一号”载人飞船与“天宫二号”成功进行对接.在对接前,“神舟十一号”的运行轨道高度为341km,“天宫二号”的运行轨道高度为393km,它们在各自轨道上作匀速圆周运动时,下列判断正确的是( )| A. | “神舟十一号”比“天宫二号”的加速度小 | |
| B. | “神舟十一号”比“天宫二号”的运行周期短 | |
| C. | “神舟十一号”比“天宫二号”运行速度小 | |
| D. | “神舟十一号”里面的宇航员受地球的吸引力为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 60:1 | B. | 16:1 | C. | 4:1 | D. | 2:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,粗细均匀且导热良好的U形管竖直放置,横截面积为S=2cm2,右端与大气相通,左端用水银柱封闭着L=50cm的气柱(可视为理想气体),左管的水银面比右管的水银面高出h1=16cm,现将U形管右端与一低压舱(图中未画出)接通,隐定后右管水银面高出左管水银面h2=4cm.若环境温度不变.大气压强p0=76cmHg.(水银的密度为13.6×103kg/m3,g取10m/s2)
如图所示,粗细均匀且导热良好的U形管竖直放置,横截面积为S=2cm2,右端与大气相通,左端用水银柱封闭着L=50cm的气柱(可视为理想气体),左管的水银面比右管的水银面高出h1=16cm,现将U形管右端与一低压舱(图中未画出)接通,隐定后右管水银面高出左管水银面h2=4cm.若环境温度不变.大气压强p0=76cmHg.(水银的密度为13.6×103kg/m3,g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
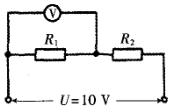 如图所示,两个定值电阻R1、R2串联后接在输出电压U恒为10V的直流电源上,有人把一个电压表并联在R1两端,电压表的示数为6V,如果将电表改接在R2两端,则电压表的示数将( )
如图所示,两个定值电阻R1、R2串联后接在输出电压U恒为10V的直流电源上,有人把一个电压表并联在R1两端,电压表的示数为6V,如果将电表改接在R2两端,则电压表的示数将( )| A. | 小于4V | B. | 等于4V | C. | 大于4V、小于6V | D. | 等于或大于6V |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,是质量m=2kg的物体在水平面上做直线运动的v-t图象,0-1s内物体受水平拉力F作用,1s未撤去F,取g=10m/V,求:
如图所示,是质量m=2kg的物体在水平面上做直线运动的v-t图象,0-1s内物体受水平拉力F作用,1s未撤去F,取g=10m/V,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com