
 ��ͼ��ʾ����ƽ��ֱ������ϵxOy�ĵڶ��������г�ǿ��СΪE����x�����������ǿ�糡���ڵ�һ��������һ�Ÿ�Ӧǿ��ΪB��Բ����ǿ�ų�����ͼ��δ���������ų�����ֱxOyƽ�棬Բ����ǿ�ų�����ı߽���x�������ڵ�P���������ӣ���������m�������q������������a��b����ȵ������ز�ͬ�����P��ͬʱ����ų���������a���ٶȷ�����y��������b���ٶȷ�����x��������ļнǦ�=30�㣬a��b�����ų���ֱ��y�����ڶ����ޣ�aͨ��y���ϵĵ�Q��OP=2OQ=2L����a��b����y���ʱ����Ϊt0����
��ͼ��ʾ����ƽ��ֱ������ϵxOy�ĵڶ��������г�ǿ��СΪE����x�����������ǿ�糡���ڵ�һ��������һ�Ÿ�Ӧǿ��ΪB��Բ����ǿ�ų�����ͼ��δ���������ų�����ֱxOyƽ�棬Բ����ǿ�ų�����ı߽���x�������ڵ�P���������ӣ���������m�������q������������a��b����ȵ������ز�ͬ�����P��ͬʱ����ų���������a���ٶȷ�����y��������b���ٶȷ�����x��������ļнǦ�=30�㣬a��b�����ų���ֱ��y�����ڶ����ޣ�aͨ��y���ϵĵ�Q��OP=2OQ=2L����a��b����y���ʱ����Ϊt0�������� ��1�����������ڴų��ж�������Բ���˶����������ǵ��˶��켣��ȷ�����켣��Ӧ��Բ�Ľǣ��о�b���ӵ��˶�ʱ�������ڵĹ�ϵ����ôŸ�Ӧǿ��B�����о�a�Ĺ켣�뾶������ٶ�v�Ĵ�С��
��2������b����糡�����ȼ���ֱ���˶����ɶ��ܶ������ڵ糡���˶���y�����Զ����x��
��3�����ݹ켣��Ӧ��Բ�Ľ��������a�ӿ�ʼ�˶�������뿪�ų������ʱ��t��
��4����ֻ���ڶ������ڵ���ǿ�糡�����Ϊ��y�Ḻ�������ӽ���糡������ƽ���˶�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�о��������˶��Ĺ��ɣ����a��b����x���ϵ������ľ����x��
��� �⣺��1�������ӵ��˶��켣��ͼ���ڴų��е��˶�����Ϊ T=$\frac{2��m}{qB}$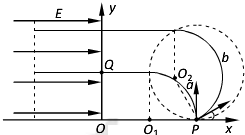
a�����ڴų���ת��90��Բ�Ľǣ��˶�ʱ��Ϊ ta=$\frac{T}{4}$
b�����ڴų���ת��150��Բ�Ľǣ��˶�ʱ��Ϊ tb=$\frac{5T}{12}$
��������t0=tb-ta=$\frac{T}{6}$
�ɵ� B=$\frac{��m}{3q{t}_{0}}$
��a�Ĺ켣��֪a�����ڴų��е��˶��뾶 R=L
��qvB=m$\frac{{v}^{2}}{R}$
�� v=$\frac{qBR}{m}$=$\frac{��L}{3{t}_{0}}$
��2�������ڵ糡�У��ɶ��ܶ����ã�
-qEx=0-$\frac{1}{2}m{v}^{2}$
��� x=$\frac{m{��}^{2}{L}^{2}}{18qE{t}_{0}^{2}}$
��3������֪������a�ӿ�ʼ�˶�������뿪�ų������ʱ�� t=ta=$\frac{T}{4}$
��t0=$\frac{T}{6}$����t=$\frac{3}{2}{t}_{0}$
��4�����ӽ���糡������ƽ���˶�������
��ֱ��λ�ƴ�С�ֱ�Ϊ ha=L��hb=R+Rcos30��=$\frac{2+\sqrt{3}}{2}$L
��ha=$\frac{1}{2}a{t}_{a1}^{2}$��hb=$\frac{1}{2}a{t}_{b1}^{2}$��xa=vata1��xb=vbtb1��
��a=$\frac{qE}{m}$
��a��b����x���ϵ������ľ����x=xb-xa=$\frac{��L}{3{t}_{0}}$$\sqrt{\frac{2mL}{qE}}$��$\sqrt{\frac{2+\sqrt{3}}{2}}$-1��
��
��1�������ڴų����˶��ٶ�v�Ĵ�СΪ$\frac{��L}{3{t}_{0}}$��
��2������b�ڵ糡���˶���y�����Զ����xΪ$\frac{m{��}^{2}{L}^{2}}{18qE{t}_{0}^{2}}$��
��3������a�ӿ�ʼ�˶�������뿪�ų������ʱ��tΪ$\frac{3}{2}{t}_{0}$��
��4��a��b����x���ϵ������ľ���Ϊ$\frac{��L}{3{t}_{0}}$$\sqrt{\frac{2mL}{qE}}$��$\sqrt{\frac{2+\sqrt{3}}{2}}$-1����
���� �����������Ƚ���ų�������Բ���˶������ڵ糡������ƽ���˶���Ҫע�������켣�����ӵ㣬�����˶��켣���ɼ��ι�ϵ��Բ�Ľ��ǹؼ���Ȼ������˶�ѧ��ʽ��ţ�ٵڶ������Լ����ι�ϵ��ʽ��⣮


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 9cm 100N/m | B�� | 10cm 90N/m | C�� | 15cm 60N/m | D�� | 12cm 30N/m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
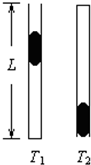 ��ͼ��ʾ��һ��ֱ���õġ���ΪL��ϸ���¶˷�գ��϶����������Ϊ�������壩��ͨ����ʼʱ���������¶�ΪT1������һ��ˮ�����ӹܿڿ�ʼע����ڽ�������գ��ù����������¶ȱ��ֲ�����û������©����ƽ�����������������������ȱ�Ϊ1��3�����������²������¶Ƚ���T2���ڱ����¶Ȳ���������½��ܵ��ã�ƽ���ˮ�����¶�����¶˸պ�ƽ�루û��ˮ��©��������֪T1=2.5T2������ѹǿΪP0���������ٶ�Ϊg����ˮ�����ij���h��ˮ�����ܶȦѣ�
��ͼ��ʾ��һ��ֱ���õġ���ΪL��ϸ���¶˷�գ��϶����������Ϊ�������壩��ͨ����ʼʱ���������¶�ΪT1������һ��ˮ�����ӹܿڿ�ʼע����ڽ�������գ��ù����������¶ȱ��ֲ�����û������©����ƽ�����������������������ȱ�Ϊ1��3�����������²������¶Ƚ���T2���ڱ����¶Ȳ���������½��ܵ��ã�ƽ���ˮ�����¶�����¶˸պ�ƽ�루û��ˮ��©��������֪T1=2.5T2������ѹǿΪP0���������ٶ�Ϊg����ˮ�����ij���h��ˮ�����ܶȦѣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����������Ϊ M=$\frac{{4{��^2}{r_2}}}{GT_1^2}$ | |
| B�� | �����������������ٶ�Ϊg=$\frac{4{��}^{2}{r}_{1}}{{T}_{1}}$ | |
| C�� | ��½���ڰ뾶Ϊr2�������Բ���˶�������ΪT2=T1$\frac{\sqrt{{{r}_{2}}^{3}}}{\sqrt{{{r}_{1}}^{3}}}$ | |
| D�� | ��½����r1��r2������˶�ʱ���ٶȴ�С֮��Ϊ$\frac{{v}_{1}}{{v}_{2}}$=$\sqrt{\frac{{m}_{1}{r}_{2}}{{m}_{2}{r}_{1}}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
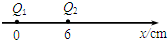 ��ͼ��ʾ�����������������Q1=+4.0��10-8C��Q2=-10-8C���ֱ�̶���x�������x=0��x=6cm��λ���ϣ�ȡ����Զ�����Ϊ�㣮������˵����ȷ���ǣ�������
��ͼ��ʾ�����������������Q1=+4.0��10-8C��Q2=-10-8C���ֱ�̶���x�������x=0��x=6cm��λ���ϣ�ȡ����Զ�����Ϊ�㣮������˵����ȷ���ǣ�������| A�� | ������Զ�⣬x��������ֻ��һ���糡ǿ��Ϊ��ĵ� | |
| B�� | x�������ϵ糡ǿ�ȷ�����x�������������ǣ�0��6cm���ͣ�12cm���ޣ� | |
| C�� | ��x=3cm��x����д�����һ�������� | |
| D�� | ��x����x��6cm�������Ʀգ�0�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ס���������ͬһ��������ͬʱ��ʼ�ɺӣ�M��N�ֱ��Ǽס��������ij����㣬����ͷ��Ӱ����ɦ��ǣ��״���ͷǡ�ö�N�������P�㣬����һ��ʱ���Ҵ�ǡ�õ���P�㣬��������ٶȴ�С��ͬ����������������Ӱ����Եĺ��У������ж���ȷ���ǣ�������
��ͼ��ʾ���ס���������ͬһ��������ͬʱ��ʼ�ɺӣ�M��N�ֱ��Ǽס��������ij����㣬����ͷ��Ӱ����ɦ��ǣ��״���ͷǡ�ö�N�������P�㣬����һ��ʱ���Ҵ�ǡ�õ���P�㣬��������ٶȴ�С��ͬ����������������Ӱ����Եĺ��У������ж���ȷ���ǣ�������| A�� | �״�Ҳ�ܵ������� | B�� | �����ɺ�ʱ�䲻��� | ||
| C�� | ����������NPֱ���� | D�� | �ɺӹ����������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���Ӽ����Ϊƽ�����ʱ�����Ӽ�������Ϊ�㣬������������� | |
| B�� | ���嶼��Ȼ���й���ļ�����״ | |
| C�� | �����ۻ�ʱ��������������ƽ�����ܲ��� | |
| D�� | �¶���ͬ���������ƽ������һ����ͬ�������������˶���ƽ�����ʲ�һ����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
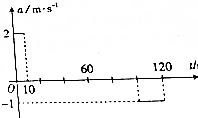 һ�������ɾ�ֹ��ʼ�ر�ֱ�Ĺ�·�Ӽ��˶����ҵأ����˶��ļ��ٶ���ʱ��仯�Ĺ�ϵ��ͼ����
һ�������ɾ�ֹ��ʼ�ر�ֱ�Ĺ�·�Ӽ��˶����ҵأ����˶��ļ��ٶ���ʱ��仯�Ĺ�ϵ��ͼ�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com