
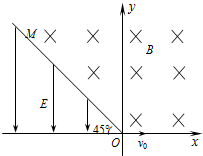
 在xOy平面内,直线OM与x轴负方向成45°角,以OM为边界的匀强电场和匀强磁场如图所示.在坐标原点O有一不计重力的粒子,其质量和电荷量分别为m和+q,以v0沿x轴正方向运动,粒子每次到x轴将反弹,第一次无能量损失,以后每次反弹水平分速度不变,竖直分速度大小减半、方向相反.电场强度E和磁感应强度B关系为B=$\frac{m{v}_{0}}{q}$、E=$\frac{m{{v}_{0}}^{2}}{16q}$.求带电粒子:
在xOy平面内,直线OM与x轴负方向成45°角,以OM为边界的匀强电场和匀强磁场如图所示.在坐标原点O有一不计重力的粒子,其质量和电荷量分别为m和+q,以v0沿x轴正方向运动,粒子每次到x轴将反弹,第一次无能量损失,以后每次反弹水平分速度不变,竖直分速度大小减半、方向相反.电场强度E和磁感应强度B关系为B=$\frac{m{v}_{0}}{q}$、E=$\frac{m{{v}_{0}}^{2}}{16q}$.求带电粒子:分析 (1)粒子在磁场中做匀速圆周运动,由牛顿第二定律求出粒子轨道半径,然后求出坐标位置.
(2)粒子在电场中加速,由动能定理可以求出粒子的动能.
(3)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出粒子的总路程.
解答 解:(1)粒子进入磁场,根据左手定则,粒子做$\frac{3}{4}$的圆周运动后经过OM,
根据洛伦兹力提供向心力有:$qvB=m\frac{v^2}{R}$,
代入数据解得:R=1m,
故第一次经过OM时的坐标为(-1m、1m);
(2)粒子第二次进入磁场,速度不变,则粒子在磁场中运动的半径也为R,
故进入电场时离x轴的高度为2R,根据动能定理,粒子到达x轴的动能有:
$2qER=\frac{1}{2}m{v^2}-\frac{1}{2}m{v_0}^2$,
解得,动能为:${E_k}=\frac{1}{2}m{v^2}=\frac{5}{8}mv_0^2$;
(3)粒子运轨迹如图所示: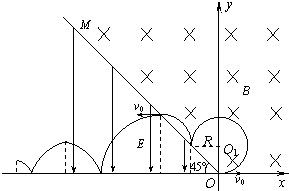
因粒子第二次进入电场做类平抛运动,故到达x轴时的水平分速度为v0,
竖直方向:$a=\frac{qE}{m}$${v_y}^2=2a{h_1}$
解得:${v_y}=\frac{v_0}{2}$,
从类平抛开始,粒子第一次到达最高点离x轴的竖直高度为:${h_1}=\frac{v_y^2}{2a}$
第二次到达最高点离x轴的竖直高度为:${h_2}=\frac{{{{(\frac{v_y}{2})}^2}}}{2a}=\frac{{{v_y}^2}}{2a}{(\frac{1}{2})^2}$
…
第n次到达最高点离x轴的竖直高度为:${h_n}=\frac{{{v_y}^2{{(\frac{1}{2})}^{2n}}}}{2a}=\frac{{{v_y}^2}}{2a}{(\frac{1}{2})^{2n}}$
故从类平抛开始,在竖直方向上往返的总路程为:$h=\frac{v_y^2}{2a}+2×\frac{v_y^2}{2a}[{(\frac{1}{2})^2}+{(\frac{1}{2})^4}…+{(\frac{1}{2})^{2n}}]=\frac{5v_y^2}{6a}=\frac{{10m{v_0}}}{3qB}=\frac{10}{3}$
故在电场中运动的竖直方向上总路程:$h'=2R+h=\frac{{16m{v_0}}}{3qB}=\frac{16}{3}$m;
答:(1)第一次经过OM时的坐标为(-1m、1m);
(2)第二次到达x轴的动能为$\frac{5}{8}$mv02;
(3)在电场中运动时竖直方向上的总路程为$\frac{16}{3}$m.
点评 本题考查了粒子在磁场与电场中的运动,分析清楚粒子运动过程是正确解题的关键,粒子在磁场中做匀速圆周运动,在电场中做类平抛运动,应用牛顿第二定律与类平抛运动规律即可正确解题.


科目:高中物理 来源: 题型:选择题
| A. | 3J | B. | 30J | C. | 300J | D. | 3000J |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
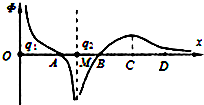 如图所示,在x轴上的O、M两点同定着两个电荷量分别为q1和q2的点电荷,两电荷连线上各点电势Φ随x的变化关系如图,其中A、B两点的电势均为零,BD段中的C点离x轴最远,则( )
如图所示,在x轴上的O、M两点同定着两个电荷量分别为q1和q2的点电荷,两电荷连线上各点电势Φ随x的变化关系如图,其中A、B两点的电势均为零,BD段中的C点离x轴最远,则( )| A. | q1为正电荷、q2为负电荷 | |
| B. | BD段中C点场强最大且沿x轴正方向 | |
| C. | A点场强小于C点场强 | |
| D. | 将一负点电荷从B点移到D点,电场力先做正功后做负功 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
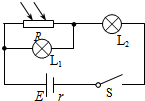 如图所示电路中,L1、L2为两只相同灯泡,R为光敏电阻,当光照强度逐渐增强的过程中,下列判断正确的是( )
如图所示电路中,L1、L2为两只相同灯泡,R为光敏电阻,当光照强度逐渐增强的过程中,下列判断正确的是( )| A. | L1、L2两灯均逐渐变暗 | |
| B. | L1灯逐渐变暗,L2灯逐渐变亮 | |
| C. | 电源内电路消耗功率逐渐增大 | |
| D. | 光敏电阻R和灯泡L1消耗的总功率逐渐增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 氢原子从n=4的状态跃迁到n=2的状态时,发射出光子 | |
| B. | 一束光照射到某种金属上不能发生光电效应,是因为该束光的波长太短 | |
| C. | 高速运动的质子、中子和电子都具有波动性 | |
| D. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能增大,原子总能量减小. |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 可求出乙车追上甲车时,乙车的速度 | |
| B. | 不能求出乙车追上甲车时,乙车的速度 | |
| C. | 可求出乙车从开始运动到追上甲车时,乙车运动的时间 | |
| D. | 不能求出乙车从开始运动到追上甲车时,乙车运动的时间 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 水平方向恒力F将一个质量为5kg的木块压在竖直墙壁上,如图,木块与墙壁之间的摩擦系数μ=0.2,要使木块沿竖直方向匀速下滑,那么作用力F的值是多少?
水平方向恒力F将一个质量为5kg的木块压在竖直墙壁上,如图,木块与墙壁之间的摩擦系数μ=0.2,要使木块沿竖直方向匀速下滑,那么作用力F的值是多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 测定电源的电动势和内电阻的实验电路和U-I图象如下,回答下列问题:
测定电源的电动势和内电阻的实验电路和U-I图象如下,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com