
 ��ͼ��ʾ����xOyƽ��ĵڢ�����ijһ�����д�ֱ��ֽ���������ǿ�ų�B1���ų�����ı߽�Ϊ��Բ�Σ���һ����m=10-12kg��������q=10-7C��a���Ӵ�O�����ٶ�v0=105m/s������y��������ɦ�=30������ڢ����ޣ����ų�ƫת���y���ϵ�P�㴹ֱ��y������ų�����ڢ����ޣ�P��������ΪyP=3m��y���Ҳ�ʹ�ֱ��x�������������ƽ����y��ָ��y�Ḻ�������ǿ�糡��a���ӽ���������x�ύ��Q����ڢ����ޣ�Q�������xQ=6$\sqrt{3}$m�������Ҳ��д�ֱֽ���������ǿ�ų�B2����Ÿ�Ӧǿ�ȴ�СB2=B1���������ӵ���������
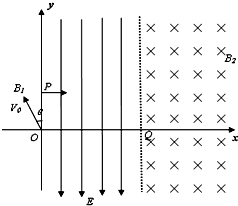
��ͼ��ʾ����xOyƽ��ĵڢ�����ijһ�����д�ֱ��ֽ���������ǿ�ų�B1���ų�����ı߽�Ϊ��Բ�Σ���һ����m=10-12kg��������q=10-7C��a���Ӵ�O�����ٶ�v0=105m/s������y��������ɦ�=30������ڢ����ޣ����ų�ƫת���y���ϵ�P�㴹ֱ��y������ų�����ڢ����ޣ�P��������ΪyP=3m��y���Ҳ�ʹ�ֱ��x�������������ƽ����y��ָ��y�Ḻ�������ǿ�糡��a���ӽ���������x�ύ��Q����ڢ����ޣ�Q�������xQ=6$\sqrt{3}$m�������Ҳ��д�ֱֽ���������ǿ�ų�B2����Ÿ�Ӧǿ�ȴ�СB2=B1���������ӵ������������� ��1��a�����ڵ糡������ƽ���˶���ץס�����ڴ�ֱ�糡����������ֱ���˶����ص糡�������ȼ���ֱ���˶������ţ�ٵڶ����ɺ��˶�ѧ��ʽ����糡ǿ�ȵĴ�С��
��2�����������ڴų��е��˶��켣����ϼ��ι�ϵ����뾶�����ݰ뾶��ʽ����Ÿ�Ӧǿ�ȣ�ͨ�����ι�ϵ�����Բ�δų�����B1����С���S��
��3��a��b���ӽ�����ӭ����������a���Ӿ����ų�B2ƫת����b������ײ����������Ӵ�O�㾭���ų�B1���糡���ų�B2���ʱ���Լ��뿪�ų�B2������㣻����ڵ糡�е��˶���Ϊx����ķ��˶���y����ķ��˶���ʽ������λ�ƹ�ϵ��ʱ���ϵ��ʽ��������⣮
��� �⣺��1��a�����ڵ糡������ƽ���˶����˶�ʱ��Ϊt
xQ=v0t ��
${y}_{P}=\frac{1}{2}a{t}^{2}$ ��
a=$\frac{qE}{m}$ ��
�ɢ٢ڢ۽��E=5.56��103N/C��
��2��a�����ڴų�B1��������Բ���˶����켣��ͼ��ʾ���뾶ΪR1��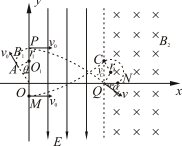
��ͼ��֪��${y}_{P}={R}_{1}+\frac{{R}_{1}}{sin��}$ ��
�������ݽ��R1=1m��
$q{v}_{0}{B}_{1}=m\frac{{{v}_{0}}^{2}}{{R}_{1}}$ ��
�ɢܢݽ��B1=1T��
���������A�����ų�B1��AP���е�Ϊ��С��Բ�ų������Բ�ģ��뾶Ϊr��
r=Rsin60�� ��
��Բ�δų�����B1����С���$s=\frac{1}{2}��{r}^{2}=\frac{3}{8}��\\;{m}^{2}$m2
��3����a������A�����ų�B2ʱ���ٶ�v��x��ļн�Ϊ��������뾶ΪR2����
$tan��=\frac{at}{{v}_{0}}$ ��
��=30��
$v=\frac{{v}_{0}}{cos��}$ ��
${R}_{2}=\frac{mv}{q{B}_{2}}=\frac{2\sqrt{3}}{3}m$ ��
��������ڴų�B2�е������Ϊc�����������֪b������a������B2����ӭ����������켣��a���ӹ켣ǡ�öԳƣ�����b�����ڴų�B2�е������Ϊc���뾶R3=R2��
�������ڴų����˶�������T=$\frac{2��m}{qB}$ ��10��
����a��B1��B2����Բ���˶�������T1��T2��b������B2����Բ���˶�������T3�Ĺ�ϵ�ǣ�T1��T2��T3��a������B1���˶�ʱ��Ϊ$t��=\frac{{T}_{1}}{3}$��
���ԣ���a���ӵ�Q��ʱ��b�����ڴų������˶���${t}_{1}=\frac{{T}_{2}}{3}$���������ڸ����˶�����֮һ���ڼ���������a��b����������N�ǹ켣��x��Ľ��㣮
${x}_{N}={x}_{Q}+2{R}_{2}cos��\frac{��}{2}-����$ ��11��
���${x}_{N}=\frac{20\sqrt{3}}{3}m$��
������N��������$\frac{20\sqrt{3}}{3}$m��0m����
�𣺣�1����ǿ�糡�ĵ糡ǿ��E�Ĵ�СΪ5.56��103N/C��
��2����Բ�δų��Ÿ�Ӧǿ��B1�Ĵ�С1T����С���Ϊ$\frac{3}{8}��{m}^{2}$��
��3��N���������$\frac{20\sqrt{3}}{3}$m��0m����
���� ����ؼ�����ȷ���ӵ��˶����ɣ�Ҫ�ֹ��̻������ӵ��˶��켣��Ȼ������ţ�ٵڶ����ɡ���ƽ���˶��ķ��˶���ʽ���˶�ѧ��ʽ��ʽ��⣻���⼸�ι�ϵ��Ϊ���ӣ�����Ϊ�����塢����̡�����ɣ��ǵ��͵ġ����ࡱ���⣻���ѣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
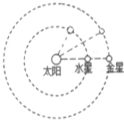 ��ˮ�Ǻͽ�����̫�����˶���ΪԲ���˶�����ˮ������Ǻ�̫����һ��ֱ���Ͽ�ʼ��ʱ�����������ͬ��ʱ����ˮ�ǡ�����ת���ĽǶȷֱ�Ϊ��1����2����Ϊ��ǣ������ɴ����������ˮ�Ǻͽ��ǵ� ��������
��ˮ�Ǻͽ�����̫�����˶���ΪԲ���˶�����ˮ������Ǻ�̫����һ��ֱ���Ͽ�ʼ��ʱ�����������ͬ��ʱ����ˮ�ǡ�����ת���ĽǶȷֱ�Ϊ��1����2����Ϊ��ǣ������ɴ����������ˮ�Ǻͽ��ǵ� ��������| A�� | �ܶ�֮�� | B�� | ��̫���ľ���֮�� | ||
| C�� | ��̫�������ٶ�֮�� | D�� | ��̫��������֮�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
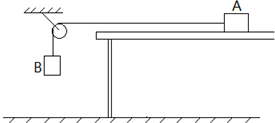 ����ͼ��ʾ��װ�ò������A��ˮƽ�����Ķ�Ħ�������������A����ˮƽ�����ϣ��������ƹ����ʶ����������B���������������������������뻬�ּ��Ħ���������ƿ���������ʵ��ʱ������A��ϸ��������������ƽ�У���ѹס���AʹB�����Ȼ������ϵͳ�ȶ������׳߲����ʱ���B�������ĸ߶�h��Ȼ���ɾ�ֹ�ͷ�A��B�������A�˶���B��غ�ֹͣ�����A�����������ϻ���һ�ξ����ͣ�������ϣ�Ϊ������A��ˮƽ�����Ķ�Ħ����������ʵ�黹��Ҫ��������������A��B������������A�˶����ܾ��룬���׳����Ҫ�IJ�����������ƽ�����Ħ�������ı���ʽΪ ��=$\frac{{m}_{B}h}{��{m}_{A}+{m}_{B}��s+{m}_{B}h}$��ʽ�и����ŵ�������mA��mB�ֱ�ΪA��B��������sΪ����A�˶����ܾ��룮
����ͼ��ʾ��װ�ò������A��ˮƽ�����Ķ�Ħ�������������A����ˮƽ�����ϣ��������ƹ����ʶ����������B���������������������������뻬�ּ��Ħ���������ƿ���������ʵ��ʱ������A��ϸ��������������ƽ�У���ѹס���AʹB�����Ȼ������ϵͳ�ȶ������׳߲����ʱ���B�������ĸ߶�h��Ȼ���ɾ�ֹ�ͷ�A��B�������A�˶���B��غ�ֹͣ�����A�����������ϻ���һ�ξ����ͣ�������ϣ�Ϊ������A��ˮƽ�����Ķ�Ħ����������ʵ�黹��Ҫ��������������A��B������������A�˶����ܾ��룬���׳����Ҫ�IJ�����������ƽ�����Ħ�������ı���ʽΪ ��=$\frac{{m}_{B}h}{��{m}_{A}+{m}_{B}��s+{m}_{B}h}$��ʽ�и����ŵ�������mA��mB�ֱ�ΪA��B��������sΪ����A�˶����ܾ��룮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ס����ǹ����ͬ�ĵ��ݣ���������a��b�ӵ�ѹΪU��ֱ����Դʱ�����۵�Դ����������һ���������������ƾ����������⣬�ҵƾ���������a��b�ӵ�ѹ����ЧֵΪU�Ľ�����Դʱ���Ʒ������Ĺ⣬�ҵ����������⣮������ƴ�����Ԫ��x�����ҵƴ�����Ԫ��y�������ж���ȷ���ǣ�������
��ͼ��ʾ���ס����ǹ����ͬ�ĵ��ݣ���������a��b�ӵ�ѹΪU��ֱ����Դʱ�����۵�Դ����������һ���������������ƾ����������⣬�ҵƾ���������a��b�ӵ�ѹ����ЧֵΪU�Ľ�����Դʱ���Ʒ������Ĺ⣬�ҵ����������⣮������ƴ�����Ԫ��x�����ҵƴ�����Ԫ��y�������ж���ȷ���ǣ�������| A�� | x�����ǵ����Ȧ��y�����ǵ����� | B�� | x�����ǵ�������y�����ǵ����Ȧ | ||
| C�� | x�����Ƕ����ܣ�y�����ǵ����� | D�� | x�����ǵ����Ȧ��y�����Ƕ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
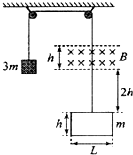 ��ͼ��ʾ������Ϊ3m��������һ����Ϊm�ĵ��߿���һ����Եϸ���������������������߶���ͬ�Ķ������ϣ���֪���߿����ΪR����߱߳�ΪL����һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB���ų����±߽�ľ��롢���߿���ֱ�߳���Ϊh����ʼʱ�̣��ų����±�Ե�͵��߿��ϱ�Ե�ĸ߶Ȳ�Ϊ2h��������Ӿ�ֹ��ʼ�ͷţ����߿���ٽ���ų����ڵ��߿��ų�ǰ�Ѿ�������ֱ���˶�������������Ħ�����������ƣ��������ٶ�Ϊg��������˵������ȷ���ǣ�������
��ͼ��ʾ������Ϊ3m��������һ����Ϊm�ĵ��߿���һ����Եϸ���������������������߶���ͬ�Ķ������ϣ���֪���߿����ΪR����߱߳�ΪL����һ��ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB���ų����±߽�ľ��롢���߿���ֱ�߳���Ϊh����ʼʱ�̣��ų����±�Ե�͵��߿��ϱ�Ե�ĸ߶Ȳ�Ϊ2h��������Ӿ�ֹ��ʼ�ͷţ����߿���ٽ���ų����ڵ��߿��ų�ǰ�Ѿ�������ֱ���˶�������������Ħ�����������ƣ��������ٶ�Ϊg��������˵������ȷ���ǣ�������| A�� | ���߿�ս���ų�ʱ���ٶ�Ϊv=2$\sqrt{gh}$ | |
| B�� | ���߿����ų�����ijһʱ�̵��ٶ�Ϊv�����ʱ����ļ��ٶ�Ϊa=$\frac{1}{2}$g-$\frac{{B}^{2}{L}^{2}v}{4mR}$ | |
| C�� | ���߿��ų�ʱ���ٶ�Ϊ$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| D�� | ���߿�ͨ���ų��Ĺ����в���������Q=8mgh-$\frac{8{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������5sʱָ����������5sĩ��һʱ�� | |
| B�� | ������5s��ָ����������4sĩ��5sĩ��1s��ʱ�� | |
| C�� | �����ڵ�5s��ָ����������4sĩ��5sĩ��1s��ʱ�� | |
| D�� | ��4sĩ���ǵ�5s����ָ����ʱ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 1W | B�� | 10W | C�� | 100W | D�� | 1000W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
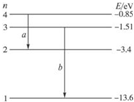
| A�� | ���ڷų����ӣ�ԭ�ӵ��������� | |
| B�� | ����a���������ڹ���b������ | |
| C�� | ����a�IJ������ڹ���b�IJ��� | |
| D�� | ������a��ʹij�����������ЧӦ�������bһ����ʹ�ý����������ЧӦ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | �糡ǿ�ȱȽ���EA��EB | |
| B�� | ���ƱȽ��Ǧ�A����B | |
| C�� | ���Ʋ�Ƚ���UAB=UBC | |
| D�� | ��������AC�����ƶ��糡�������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com