
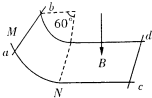
 如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:
如图所示,两根间距为l的光滑金属导轨(不计电阻),由一段圆弧部分与一段无限长的水平段部分组成.其水平段加有方向竖直向下的匀强磁场,其磁感应强度为B,导轨水平段上静止放置一金属棒cd,质量为2m,电阻为2r.另一质量为m,电阻为r的金属棒ab,从圆弧段M处由静止释放下滑至N处进入水平段,圆弧段MN半径为R,所对圆心角为60°,求:| 1 |
| 2 |
| gR |
| E |
| 2r+r |
Bl
| ||
| 3r |
| 1 |
| 3 |
| gR |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| gR |
Bl
| ||
| 3r |
| 1 |
| 3 |
| gR |
| 1 |
| 3 |


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中物理 来源: 题型:
 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆能刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )
如图所示,两根间距为d的平行光滑金属导轨间接有电源E,导轨平面与水平面间的夹角θ=30°.金属杆ab垂直导轨放置,导轨与金属杆接触良好.整个装置处于磁感应强度为B的匀强磁场中.当磁场方向垂直导轨平面向上时,金属杆ab刚好处于静止状态.要使金属杆能沿导轨向上运动,可以采取的措施是( )查看答案和解析>>
科目:高中物理 来源: 题型:
| v0 |
| 2 |
| 2v1 |
| 3 |
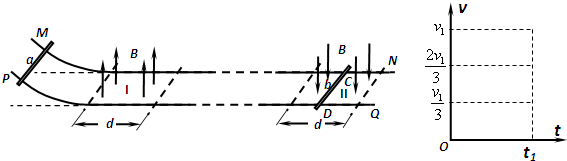
查看答案和解析>>
科目:高中物理 来源: 题型:
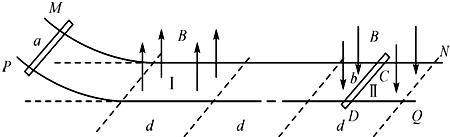
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com