
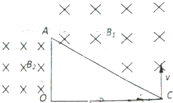
 有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求:
有一直角三角形OAC,OC长为12cm,∠C=30°,AC上方存在垂直纸面向里的匀强磁场,磁感应强度B1=1T,OA左侧也存在垂直纸面向里的匀强磁场,磁感应强度大小B2未知,一质量为m=8×10-10kg、电荷量q=1×10-4C的带正电粒子从C点以垂直于OC的速度v进入磁场,恰好经A点到达O点,不计粒子重力,求:分析 (1)粒子在磁场B1中做匀速圆周运动,画出运动的轨迹,画出运动的轨迹,由几何关系求出半径,然后由洛伦兹力提供向心力,结合牛顿第二定律得出磁场B2的大小;
(2)由周期公式与偏转角度之间的关系即可求出时间.
解答 解:(1)粒子在磁场B1中做匀速圆周运动,画出运动的轨迹如图,其圆心为O1,设轨迹半径为r1,则∠O1AC=∠O1CA=30°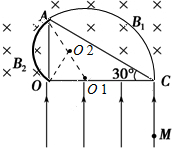
所以:∠AO1O=2∠O1CA=60°,粒子的偏转角是120°
由几何关系得:r1+r1cos60°=$\overline{OC}$
所以:r1=$\frac{2}{3}\overline{OC}$=$\frac{2}{3}$×12cm=8cm
由洛伦兹力提供向心力得:qvB1=m$\frac{{v}^{2}}{{r}_{1}}$
所以:v=$\frac{q{B}_{1}{r}_{1}}{m}$=1.0×104m/s
粒子在磁场B2中做匀速圆周运动,画出运动的轨迹如图,其圆心为O2,设轨迹半径为r2,则
$\overline{AO}$=2r2•cos∠OAO1=2r2•cos30°=$\sqrt{3}$r2
所以:r2=$\frac{\sqrt{3}}{3}$$\overline{AO}$=$\frac{\sqrt{3}}{3}•\overline{OC}•$tan30°=$\frac{1}{3}$×12cm=4cm
由洛伦兹力提供向心力得:qvB2=$\frac{m{v}^{2}}{{r}_{2}}$
所以:B2=$\frac{mv}{q{r}_{2}}$
代入数据得:B2=2T
(2)粒子在磁场B1中运动的周期:T1=$\frac{2π{r}_{1}}{v}$=$\frac{2πm}{q{B}_{1}}$
由偏转角与偏转时间的关系得:t1=$\frac{120°}{360°}$T1=$\frac{2πm}{3q{B}_{1}}$
粒子在磁场B1中运动的周期:T2=$\frac{2π{r}_{2}}{v}$=$\frac{2πm}{q{B}_{2}}$
由图可知,粒子 在磁场B2中偏转的角度也是120°
所以:t2=$\frac{1}{3}$T2=$\frac{2πm}{3q{B}_{2}}$
粒子在磁场中运动的总时间:t=t1+t2
代入数据得:t=8π×10-6s
答:
(1)未知匀强磁场的磁感应强度B2的大小是2T;
(2)粒子在磁场中运动的总时间是8π×10-6s.
点评 考查带电粒子在磁场中做匀速圆周运动的过程中,用牛顿第二定律与运动学公式,并结合几何关系来处理这两种运动,强调并突出准确的运动轨迹图.


科目:高中物理 来源: 题型:多选题
 目前世界上正研究的一种新型发电机叫磁流体发电机,如图表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体来说呈中性)沿如图所示方向射入磁场,磁场中有两块金属板A、B,这时金属板上就聚集了电荷.在磁极配置如图中所示的情况下,下列说法正确的是( )
目前世界上正研究的一种新型发电机叫磁流体发电机,如图表示它的发电原理:将一束等离子体(即高温下电离的气体,含有大量带正电和带负电的微粒,而从整体来说呈中性)沿如图所示方向射入磁场,磁场中有两块金属板A、B,这时金属板上就聚集了电荷.在磁极配置如图中所示的情况下,下列说法正确的是( )| A. | A板带正电 | |
| B. | 有电流从b经用电器流向a | |
| C. | 金属板A、B间的电场方向向下 | |
| D. | 等离子体发生偏转的原因是离子所受洛伦兹力大于所受静电力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
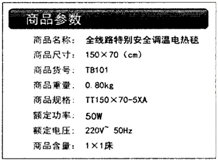 入冬以来,电热毯在网上热销.它耗电量少、温度可调节、使用方便,主要用于人们睡眠时提高被窝里的温度来达到取暖目的,还可用于被褥的去潮除湿.它将特制的、绝缘性能达到标准的软索式电热元件呈盘蛇状缝入毛毯里,通电时即发出热量,且电热元件的电阻值保持不变.如右图为某款电热毯说明书中提供的商品参数,下列说法错误的是( )
入冬以来,电热毯在网上热销.它耗电量少、温度可调节、使用方便,主要用于人们睡眠时提高被窝里的温度来达到取暖目的,还可用于被褥的去潮除湿.它将特制的、绝缘性能达到标准的软索式电热元件呈盘蛇状缝入毛毯里,通电时即发出热量,且电热元件的电阻值保持不变.如右图为某款电热毯说明书中提供的商品参数,下列说法错误的是( )| A. | 该电热毯在工作时额定电流约为0.23A | |
| B. | 该电热毯中的电热元件电阻为968Ω | |
| C. | 该电热毯在额定电压下工作一小时产生热量为50J | |
| D. | 该电热毯在额定电压下工作一小时所耗电能为0.05kWh |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
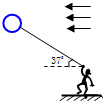 如图所示,某人用轻绳牵住一只质量m=0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成37°角.已知空气对气球的浮力为15N,人的质量M=50kg,且人受的浮力忽略.(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
如图所示,某人用轻绳牵住一只质量m=0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成37°角.已知空气对气球的浮力为15N,人的质量M=50kg,且人受的浮力忽略.(sin37°=0.6,cos37°=0.8,g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一个绝缘且内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的内径大得多),在圆管的最低点有一个直径略小于细管内径的带正电小球处于静止状态,小球的质量为m,带电量为q,重力加速度为g.空间存在一磁感应强度大小未知(不为零),方向垂直于环形细圆管所在平面且向里的匀强磁场.某时刻,给小球一方向水平向右,大小为V0=$\sqrt{5gR}$的初速度,则以下判断正确的是( )
如图所示,一个绝缘且内壁光滑的环形细圆管,固定于竖直平面内,环的半径为R(比细管的内径大得多),在圆管的最低点有一个直径略小于细管内径的带正电小球处于静止状态,小球的质量为m,带电量为q,重力加速度为g.空间存在一磁感应强度大小未知(不为零),方向垂直于环形细圆管所在平面且向里的匀强磁场.某时刻,给小球一方向水平向右,大小为V0=$\sqrt{5gR}$的初速度,则以下判断正确的是( )| A. | 无论磁感应强度大小如何,获得初速度瞬间,小球在最低点一定受到管壁的弹力作用 | |
| B. | 无论磁感应强度大小如何,小球一定能到达环形细管的最高点,且小球在最高点一定受到管壁的弹力作用 | |
| C. | 小球在从环形细圆管的最低点运动 到所能到达的最高点过程中,水平方向分速度的大小一直减小 | |
| D. | 无论磁感应强度大小如何,小球一定能到达环形细管的最高点,且小球到达最高点时的速度大小都相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
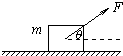 如图所示,在水平面上有一质量为m的物体,物体与水平面间的动摩擦因数为μ.
如图所示,在水平面上有一质量为m的物体,物体与水平面间的动摩擦因数为μ.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,ab是水平面上一个圆形线圈的直径,在过ab的竖直平面内有一根通电导线ef,他们不平行,当导线中的电流变大的时候,线圈的磁通量将( )
如图所示,ab是水平面上一个圆形线圈的直径,在过ab的竖直平面内有一根通电导线ef,他们不平行,当导线中的电流变大的时候,线圈的磁通量将( )| A. | 逐渐增大 | B. | 逐渐减小 | ||
| C. | 始终为零 | D. | 不为零,但保持不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 8.33m | B. | 7m | C. | 3.33m | D. | 3m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
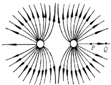 如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )
如图所示是某一电场线分布图,图中PQ两点的电场强度大小分别为EP和EQ,电势分别为φP和φQ,下列说法中正确的是( )| A. | 图示为单个正点电荷的电场线 | B. | 图示为等量异种点电荷的电场线 | ||
| C. | EP>EQ | D. | φP<φQ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com