
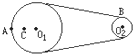
 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则( )

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中物理 来源: 题型:
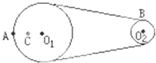 如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )
如图所示皮带转动轮,大轮直径是小轮直径的2倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑,则( )查看答案和解析>>
科目:高中物理 来源: 题型:
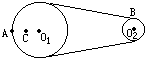 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的线速度之比vA:vB:vC=查看答案和解析>>
科目:高中物理 来源: 题型:
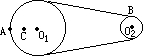 如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=
如图所示皮带转动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径.转动时皮带不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC=查看答案和解析>>
科目:高中物理 来源: 题型:
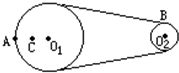 如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=
如图所示皮带转动轮,大轮直径是小轮直径的2 倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径. 转动时皮带不打滑,则A、B两点的角速度之比ωA:ωB=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com