
 图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )
图中的甲是地球赤道上的一个物体,乙是“神舟十号”宇宙飞船(周期约90min),丙是地球的同步卫星,它们运行的轨道示意图如图所示,它们都绕地心做匀速圆周运动.下列有关说法中正确的是( )| A. | 它们运动的向心加速度大小关系是a乙>a丙>a甲 | |
| B. | 它们运动的线速度大小关系是v乙<v丙<v甲 | |
| C. | 已知甲运动的周期T甲=24h,可计算出地球的密度ρ=$\frac{3π}{G{T}_{甲}^{2}}$ | |
| D. | 已知乙运动的周期T乙及轨道半径r乙,可计算出地球质量M=$\frac{4{π}^{2}{r}_{乙}^{3}}{G{T}_{乙}^{2}}$ |
分析 根据万有引力提供向心力,得出轨道半径与周期的关系,通过周期的大小比较出轨道半径的大小,从而根据万有引力提供向心力得出乙和丙的向心加速度和线速度大小关系.甲和丙的周期相同,角速度相等,根据v=rω,a=rω2,比较出甲和丙的线速度和角速度大小.根据万有引力提供向心力求出地球的质量.
解答 解:AB、根据万有引力提供向心力
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}r}{{T}^{2}}$=ma=m$\frac{{v}^{2}}{r}$,
得T=2π$\sqrt{\frac{{r}^{3}}{GM}}$
a=$\frac{GM}{{r}^{2}}$,v=$\sqrt{\frac{GM}{r}}$.
据题知,同步卫星一丙的周期为24h,大于乙的周期,则丙的轨道半径大于乙的轨道半径.
根据线速度、加速度与轨道半径的关系,知a乙>a丙,v乙>v丙.
又因为甲与丙的角速度相等,根据v=rω知,v丙>v甲,根据a=rω2知,a丙>a甲.所以有:a乙>a丙>a甲,v乙>v丙>v甲.故A正确,B错误.
C、因为甲不是卫星,它的周期与贴近星球表面做匀速圆周运动的周期不同,根据甲的周期无法求出地球的密度.故C错误.
D、对于乙,根据G$\frac{{Mm}_{乙}}{{r}_{乙}^{2}}$=m乙$\frac{{4π}^{2}}{{T}_{乙}^{2}}$r乙,
解得地球质量M=$\frac{{{4π}^{2}r}_{乙}^{3}}{{GT}_{乙}^{2}}$.故D正确.
故选:AD.
点评 解决本题的关键掌握万有引力提供向心力这一理论,知道线速度、角速度、加速度、周期与轨道半径的关系.以及知道同步卫星的特点.


科目:高中物理 来源: 题型:解答题
 如图所示质量为4kg的物体静止于水平面上,物体与水平面之间的动摩擦因数为0.5,现用一F=20N的恒力与水平方向成30°角斜向上拉物体,经过3s,该物体的位移为多少?(g=10m/s2)
如图所示质量为4kg的物体静止于水平面上,物体与水平面之间的动摩擦因数为0.5,现用一F=20N的恒力与水平方向成30°角斜向上拉物体,经过3s,该物体的位移为多少?(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 乘客做圆周运动的加速度为0.5m/s2 | |
| B. | 乘客做圆周运动的加速度为5m/s2 | |
| C. | 列车进入弯道时做匀速运动 | |
| D. | 乘客随列车运动时的速度大小不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
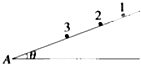 如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )
如图所示,在光滑的斜面上放置3个相同的小球(可视为质点),小球1、2、3距斜面底端A点的距离分别为x1、x2、x3,现将它们分别从静止释放,到达A点的时间分别为t1、t2、t3,斜面的倾角为θ.则下列说法正确的是( )| A. | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{3}}{{t}_{3}}$ | B. | $\frac{{x}_{1}}{{t}_{1}}$>$\frac{{x}_{2}}{{t}_{2}}$>$\frac{{x}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{x}_{1}}{{{t}_{1}}^{2}}$=$\frac{{x}_{2}}{{{t}_{2}}^{2}}$=$\frac{{x}_{3}}{{{t}_{3}}^{2}}$ | D. | 若θ增大,则$\frac{x}{{t}^{2}}$的值减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 波在介质中传播的频率由波源决定,与介质无关 | |
| B. | 如果波源停止振动,形成的波也立即停止传播 | |
| C. | 物体做机械振动,一定产生机械波 | |
| D. | 波源振动越快,波的速度越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 让小球从斜面的顶端滚下,如图所示,图中标出了不同时刻小球沿斜面滚下的位置,试粗略计算:
让小球从斜面的顶端滚下,如图所示,图中标出了不同时刻小球沿斜面滚下的位置,试粗略计算:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com