
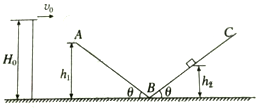
 如图所示,固定在竖直平面内倾角为θ=37°、左端高度h1=0.9m的直轨道AB,与倾角相同的足够长的直轨道BC顺滑连接(在B处有一小段光滑圆弧).其左端有一高度H0=0.972m的平台,现将一小物块(可看做质点)由平台右端以初速度v0水平抛出,恰好从A点沿AB方向进入轨道,沿轨道AB滑下,并滑上轨道BC,所能达到的最大高度h2=0.60m.若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失,已知sin37°=0.6,cos37°=0.8,求
如图所示,固定在竖直平面内倾角为θ=37°、左端高度h1=0.9m的直轨道AB,与倾角相同的足够长的直轨道BC顺滑连接(在B处有一小段光滑圆弧).其左端有一高度H0=0.972m的平台,现将一小物块(可看做质点)由平台右端以初速度v0水平抛出,恰好从A点沿AB方向进入轨道,沿轨道AB滑下,并滑上轨道BC,所能达到的最大高度h2=0.60m.若物块与两轨道间的动摩擦因数相同,不计空气阻力及连接处的能量损失,已知sin37°=0.6,cos37°=0.8,求分析 (1)物块做平抛运动,由运动的合成与分解求出落在A时的竖直分速度,然后应用匀变速直线运动与匀速运动规律求出物块的初速度.
(2)对从抛出点开始到滑上BC的最高点为研究过程,运用动能定理,求出物块与轨道间的动摩擦因数.
(3)由牛顿第二定律求出物块在斜面上的加速度,然后求出物块滑到B的时间;由牛顿第二定律求出物块在斜面BC上的加速度,最后由位移公式求出位移,从而求出P、B间的距离.
解答 解:(1)物体的初速为v0,A点速度为v,竖直速度为v1,物块在A点速度恰好沿切线方向,则v与水平线的夹角为θ=37°
由平抛运动,则:y=$\frac{1}{2}$gt12,${t}_{1}=\sqrt{\frac{2△h}{g}}=\sqrt{\frac{2×(0.972-0.9)}{10}}s=0.12$s,
对B点速度v做垂直和水平方向分解,有:v1=gt1=10×0.12=1.2m/s,
且tan37°=$\frac{{v}_{1}}{{v}_{0}}$
所以:${v}_{0}=\frac{{v}_{1}}{tan37°}=\frac{1.2}{0.75}m/s=1.6$m/s
(2)对物块从抛出点到第一次速度为零的过程,由动能定理得:
${W}_{G}-μmgcosθ(\frac{{h}_{1}}{sinθ}+\frac{{h}_{2}}{sinθ})=0-\frac{1}{2}m{v}_{0}^{2}$
化简并代入数据可得:μ=0.25
(3)滑块在A点速度为v,则$v=\sqrt{{v}_{0}^{2}+{v}_{1}^{2}}=\sqrt{1.{6}^{2}+1.{2}^{2}}m/s=2$m/s
滑块在斜面AB上受到重力、支持力和摩擦力的作用,由牛顿第二定律得:
ma1=mgsinθ-μmgcosθ
所以:${a}_{1}=\frac{mgsinθ-μmgcosθ}{m}=gsinθ-μgcosθ$=10×sin37°-0.25×10×cos37°=4m/s2
滑块滑到B时的速度:${v}_{B}^{2}-{v}^{2}=2{a}_{1}•\frac{{h}_{1}}{sinθ}$
代入数据得:vB=4m/s
A到B的时间:${t}_{2}=\frac{{v}_{B}-v}{{a}_{1}}=\frac{4-2}{4}s=0.5$s
滑块在斜面BC上受到重力、支持力和摩擦力的作用,由牛顿第二定律得:
ma2=mgsinθ+μmgcosθ
所以:${a}_{2}=\frac{mgsinθ+μmgcosθ}{m}=gsinθ+μgcosθ$=10×sin37°+0.25×10×cos37°=8m/s2
滑块滑到最高点的时间:${t}_{2}=\frac{0-{v}_{B}}{-{a}_{2}}=\frac{0-4}{-8}s=0.5$s
剩下的时间:t4=t-t1-t2-t3=1.62-0.12-0.5-0.5=0.5s
所以滑块将从最高点向下滑动,滑动时的加速度a3:${a}_{3}=\frac{mgsinθ-μmgcosθ}{m}=gsinθ-μgcosθ$=4m/s2
滑块向下滑动的距离:$x=\frac{1}{2}{a}_{3}{t}_{4}^{2}=\frac{1}{2}×4×0.{5}^{2}=0.5$m
所以P到B之间的距离为:$s=\frac{{h}_{2}}{sin37°}-x=\frac{0.6}{0.6}m-0.5m=0.5$m
答:(1)物块的初速度是1.6m/s;
(2)物块与轨道间的动摩擦因数是0.25;
(3)物块从平台右端抛出后,经时间t=1.62s运动到BC轨道上的P点(P点未标出),P、B间的距离是0.5m.
点评 本题考查了动能定理的运用、平抛运动以及牛顿运动定律的综合应用能力,关键选取适当的研究过程,根据动能定理以及牛顿第二定律列表达式进行求解.


科目:高中物理 来源: 题型:解答题
 电饭锅工作时有两种状态:一种是锅内水烧干前的加热状态,另一种是锅内水烧干后的保温状态.如图所示为电饭锅电路的示意图,S是用感温材料制造的开关,R1是电阻,R2是供加热用的电阻丝.求:
电饭锅工作时有两种状态:一种是锅内水烧干前的加热状态,另一种是锅内水烧干后的保温状态.如图所示为电饭锅电路的示意图,S是用感温材料制造的开关,R1是电阻,R2是供加热用的电阻丝.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
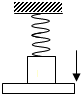 如图所示,轻质弹簧下端吊一物体,静止后弹簧的伸长量为N,现用一水平木板将物体托起使弹簧恢复到自然长度L,并保持静止,然后将木板由静止开始以加速度a(a<g)匀加速下降,直到物体与木板开始分离,求这一过程经历的时间为多少?
如图所示,轻质弹簧下端吊一物体,静止后弹簧的伸长量为N,现用一水平木板将物体托起使弹簧恢复到自然长度L,并保持静止,然后将木板由静止开始以加速度a(a<g)匀加速下降,直到物体与木板开始分离,求这一过程经历的时间为多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 1:1 | B. | 3:4 | C. | 3:1 | D. | 4:3 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 中央电视台焦点访谈节目19时40分开播 | |
| B. | 方言同学每天早上6 h起床 | |
| C. | 某女生用16 s跑完100 m | |
| D. | 天津开往德州的625次硬座普快列车于13 h 35 min从天津西站发车 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com