
 如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0.
如图所示为恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,A行星的运行轨道半径为R0、周期为T0.分析 (1)行星由恒星的万有引力提供向心力,做匀速圆周运动,根据牛顿第二定律由行星的运行轨道半径为 R0,周期为T0求出恒星O的质量;
(2)卫星绕行星做匀速圆周运动,行星对卫星的万有引力提供卫星的向心力,再由牛顿第二定律求解卫星的线速度大小;
(3)先根据多转动一圈时间为t0,求出卫星的周期;然后再根据开普勒第三定律解得轨道半径
解答 解:(1)设中央恒星O的质量为M,A行星的质量为m,则由万有引力定律和牛顿第二定律得
$G\frac{Mm}{{{R}_{0}}^{2}}=m\frac{4{π}^{2}{R}_{0}}{{{T}_{0}}^{2}}$
解得 M=$\frac{4{π}^{2}{{R}_{0}}^{3}}{{{GT}_{0}}^{2}}$
(2)设卫星的质量为m0,由题意可知:
$G\frac{m{m}_{0}}{{({r}_{0}+h)}^{2}}={m}_{0}\frac{{v}^{2}}{({r}_{0}+h)}$
$G\frac{m{m}_{0}}{{{r}_{0}}^{2}}={m}_{0}g$
解得:v=$\sqrt{\frac{g{{r}_{0}}^{2}}{{r}_{0}+h}}$
(3)由题意可知:A、B相距最近时,B对A的影响最大,且每隔时间t0发生一次最大的偏离,说明A、B相距最近,设B行星的周期为T,则有:
$(\frac{2π}{{T}_{0}}-\frac{2π}{T}){T}_{0}=2π$
解得:T=$\frac{{t}_{0}{T}_{0}}{{t}_{0}-{T}_{0}}$
据开普勒第三定律:$\frac{{R}^{3}}{{{R}_{0}}^{3}}=\frac{{T}^{2}}{{{T}_{0}}^{2}}$
解得:$R=\root{3}{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{2}}{R}_{0}$
答:(1)中央恒星O的质量为$\frac{4{π}^{2}{{R}_{0}}^{3}}{{{GT}_{0}}^{2}}$;
(2)该卫星的线速度大小为$\sqrt{\frac{g{{r}_{0}}^{2}}{{r}_{0}+h}}$;
(3)未知行星B绕中央恒星O运动的周期为$\frac{{t}_{0}{T}_{0}}{{t}_{0}-{T}_{0}}$,轨道半径为$\root{3}{{(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})}^{2}}{R}_{0}$.
点评 本题中第(1)要注意已知旋转天体的轨道半径和周期求出的是中心天体的质量,而不是旋转天体本身的质量,掌握万有引力提供向心力这一理论,并能灵活运用,知道A、B相距最近时,B对A的影响最大,且每隔时间t0发生一次最大的偏离,说明A、B相距最近,难度适中.


科目:高中物理 来源: 题型:解答题
 如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?
如图所示,质量为1t的汽车以10m/s的速度通过半径R=40m的拱桥桥顶时,车对桥顶的压力是多少?为使汽车能安全通过桥顶(汽车不脱离桥面),汽车驶上桥顶时速度不得超过多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 至少增大到原来的4倍 | B. | 至少增大到原来的2倍 | ||
| C. | 减少到原来的$\frac{2}{3}$ | D. | 减少到原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 它是人造地球卫星绕地球飞行的最小速度 | |
| B. | 它是人造地球卫星在近地圆形轨道上的运动速度 | |
| C. | 它是使卫星进入正常轨道动动的最大发射速度 | |
| D. | 它是人造地球卫星在圆形轨道上的最大环绕速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )
如图所示,叠放在一起的三个木块A、B、C一起向右运动,速度大小分别为10m/s、6m/s、8m/s,已知木块之间的接触面是粗糙的,下列关于木块之间的摩擦力的方向说法正确的是( )| A. | 木块A对木块B的摩擦力方向向右 | B. | 木块B对木块C的摩擦力方向向右 | ||
| C. | 木块A对木块C的摩擦力方向向右 | D. | 木块C对木块B的摩擦力方向向右 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 第一次做功多,功率小 | B. | 两次做功一样多,功率一样大 | ||
| C. | 第二次做功多,功率大 | D. | 两次做功一样多,第二次功率大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | hA=hB 则一定有WA=WB | B. | hA>hB 则可能有WA<WB | ||
| C. | hA<hB 则可能有WA=WB | D. | hA>hB 则一定有WA>WB |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
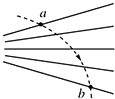 如图所示,图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受到电场力作用,根据此图不能判断是( )
如图所示,图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点,若带电粒子在运动过程中只受到电场力作用,根据此图不能判断是( )| A. | 带电粒子所带电荷的正、负 | |
| B. | 带电粒子在a、b两点的受力方向 | |
| C. | 带电粒子在a、b两点的加速度何处较大 | |
| D. | 带电粒子在a、b两点的速度何处较大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com