
分析 (1)C与B的质量相等,所以运行的规律也相等,然后结合向心力的公式即可求出C的轨道半径;
(2)三星体做圆周运动的周期T相等,写出C的向心加速度表达式即可求出.
解答 解:(1)由万有引力定律,A星受到B、C的引力的大小:FBA=FCA=$\frac{G•2{m}^{2}}{{a}^{2}}$,方向如图,
B星受到的引力分别为:${F}_{AB}=\frac{G•2{m}^{2}}{{a}^{2}}$,${F}_{CB}=\frac{G•{m}^{2}}{{a}^{2}}$,方向如图;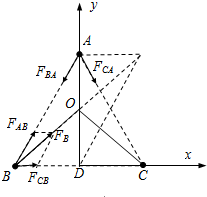
沿x方向:FBx=FABcos60°+FCB=$\frac{2G{m}^{2}}{{a}^{2}}$,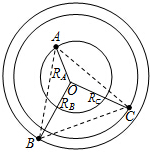
沿y方向:FBy=FABsin60°=$\frac{\sqrt{3}G{m}^{2}}{{a}^{2}}$,
可得${F}_{B}=\sqrt{{{F}_{Bx}}^{2}+{{F}_{By}}^{2}}$=$\frac{\sqrt{7}G{m}^{2}}{{a}^{2}}$,
通过对于B的受力分析可知,由于:${F}_{AB}=\frac{G•2{m}^{2}}{{a}^{2}}$,${F}_{CB}=\frac{G{m}^{2}}{{a}^{2}}$,合力的方向经过BC的中垂线AD的中点,所以圆心O一定在BC的中垂线AD的中点处.所以:
${R}_{C}={R}_{B}=\sqrt{(\frac{1}{2}a)^{2}+(\frac{\sqrt{3}}{4}a)^{2}}$=$\frac{\sqrt{7}}{4}a$.
(2)对C星:${F}_{C}={F}_{B}=\frac{\sqrt{7}G{m}^{2}}{{a}^{2}}=m{R}_{C}\frac{4{π}^{2}}{{T}^{2}}$,
解得T=$π\sqrt{\frac{{a}^{3}}{Gm}}$.
答:(1)C星体的轨道半径R为$\frac{\sqrt{7}}{4}a$;
(2)三个星体做圆周运动的周期T为$π\sqrt{\frac{{a}^{3}}{Gm}}$.
点评 该题借助于三星模型考查万有引力定律,其中B与C的质量相等,则运行的规律、运动的半径是相等的.结合万有引力定律和几何关系综合求解.


 字词句段篇系列答案
字词句段篇系列答案科目:高中物理 来源: 题型:选择题
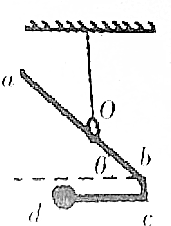 如图所示,弯折杆αbcd,在d端接一个小球,杆和球的总质量为m.一小环O套在杆ab段上用绳吊着,杆和环均处于静止状态,杆ab段与水平方向的夹角为θ,重力加速度为g,则圆环与杆的摩擦力大小为( )
如图所示,弯折杆αbcd,在d端接一个小球,杆和球的总质量为m.一小环O套在杆ab段上用绳吊着,杆和环均处于静止状态,杆ab段与水平方向的夹角为θ,重力加速度为g,则圆环与杆的摩擦力大小为( )| A. | mgtanθ | B. | mgcosθ | C. | mgsinθ | D. | mg |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略通过实验和逻辑推理说明力是维持物体运动的原因 | |
| B. | 只有在国际单位制中,牛顿第二定律的表达式才是F=ma | |
| C. | 伽利略认为自由落体运动是速度随位移均匀变化的运动 | |
| D. | 在物理问题的研究中,如果不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
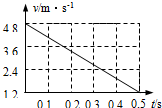 一质量m=1.0kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
一质量m=1.0kg的滑块以一定的初速度冲上一倾角为37°足够长的斜面,某同学利用传感器测出了滑块冲上斜面过程中多个时刻的瞬时速度,如图所示为通过计算机绘制出的滑块上滑过程的v-t图.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
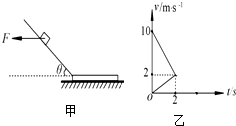 如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,木板与水平面间的摩擦因素为0.1.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平面上前2s运动的v-t图象如图乙所示,g=10m/s2.求
如图甲所示,有一倾角为30°的光滑固定斜面,斜面底端的水平面上放一质量为M的木板,木板与水平面间的摩擦因素为0.1.开始时质量为m=1kg的滑块在水平向左的力F作用下静止在斜面上,今将水平力F变为水平向右,当滑块滑到木板上时撤去力F,木块滑上木板的过程不考虑能量损失.此后滑块和木板在水平面上前2s运动的v-t图象如图乙所示,g=10m/s2.求查看答案和解析>>
科目:高中物理 来源: 题型:多选题
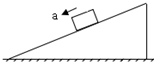 如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )
如图,粗糙的水平地面上有一质量为M的斜劈,斜劈上一质量为m的物块由静止沿斜面匀加速下滑,斜劈始终保持静止,则( )| A. | 地面对斜劈的摩擦力向右 | B. | 地面对斜劈的摩擦力向左 | ||
| C. | 斜劈对地面的压力大于(M+m)g | D. | 斜劈对地面的压力小于(M+m)g |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
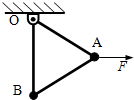 用三根轻杆做成一个边长为L的等边三角形框架,在其中两个顶点处各固定一个小球A和B,质量分别为2m和m.现将三角形框架的第三个顶点悬挂在天花板上O点,框架可绕O点自由转动.有一水平力F作用在小球A上,使OB杆恰好静止于竖直方向,则撤去F后(不计一切摩擦)( )
用三根轻杆做成一个边长为L的等边三角形框架,在其中两个顶点处各固定一个小球A和B,质量分别为2m和m.现将三角形框架的第三个顶点悬挂在天花板上O点,框架可绕O点自由转动.有一水平力F作用在小球A上,使OB杆恰好静止于竖直方向,则撤去F后(不计一切摩擦)( )| A. | 小球A和B线速度始终相同 | |
| B. | 小球A向下摆动的过程机械能守恒 | |
| C. | 小球A向下摆到最低点的过程中速度先增大后减小 | |
| D. | OB杆向左摆动的最大角度大于60° |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )| A. | $\frac{g}{2}$sinα | B. | 1.5gsinα | C. | gsinα | D. | 2gsinα |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com