
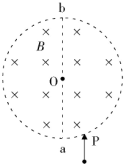
 ��ͼΪһԲ������ǿ�ų�����ĺ���棨ֽ�棩��ʾ��ͼ���Ÿ�Ӧǿ�ȴ�СΪB������ֱ��ֽ�����ڣ�һ�����Ϊq��q��0��������Ϊm��������ֱ��ab�ķ����a�����ٶ�v0����ų�������������ų�������ų�ʱ�˶������ļн�Ϊ90�㣮��������ƽ����ֱ��ab�ķ����P�������ٶ�v0����ų�����P����ab�ľ���ΪԲ�İ뾶��$\frac{1}{3}$�����Ӵ�Բ�ϵ�Q�㣨ͼ��δ�������뿪�������ֽ��ų���Ϊƽ����ֽ���Ҵ�ֱ��ֱ��ab����ǿ�糡��ͬһ������ͬ���ٶ���ֱ����P��������������Ҳ��Q���뿪����������������
��ͼΪһԲ������ǿ�ų�����ĺ���棨ֽ�棩��ʾ��ͼ���Ÿ�Ӧǿ�ȴ�СΪB������ֱ��ֽ�����ڣ�һ�����Ϊq��q��0��������Ϊm��������ֱ��ab�ķ����a�����ٶ�v0����ų�������������ų�������ų�ʱ�˶������ļн�Ϊ90�㣮��������ƽ����ֱ��ab�ķ����P�������ٶ�v0����ų�����P����ab�ľ���ΪԲ�İ뾶��$\frac{1}{3}$�����Ӵ�Բ�ϵ�Q�㣨ͼ��δ�������뿪�������ֽ��ų���Ϊƽ����ֽ���Ҵ�ֱ��ֱ��ab����ǿ�糡��ͬһ������ͬ���ٶ���ֱ����P��������������Ҳ��Q���뿪�������������������� ��1�����ݼ��ι�ϵ������������Բ���˶��Ĺ���뾶����Բ�δų��İ뾶��������ӵĹ���뾶���ɵõ�Բ�δų��İ뾶
��2�����������˶��Ĺ켣ͼ�����ݼ��ι�ϵ���PQ�����ľ���
��3�������ڵ糡������ƽ���˶���������ƽ���˶��Ĺ�������ǿ�糡�ij�ǿ
��� �⣺��1���������֪��Բ�δų��뾶R���������˶��Ĺ���뾶r��R=r
��ţ�ٵڶ����������������Ĺ�ʽ�ã�
$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{r}$
���$r=\frac{m{v}_{0}^{\;}}{qB}$
��������Բ�δų��İ뾶$R=\frac{m{v}_{0}^{\;}}{qB}$
��2���ɼ��ι�ϵ��֪ͼ�е��ı���OPO��QΪ���Σ���OQ��ֱ��ֱ��ab����ͼ��ʾ��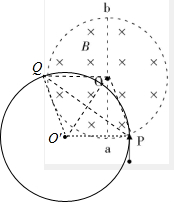
�ɼ��ι�ϵ��֪��$OO��=\sqrt{{R}_{\;}^{2}-��\frac{R}{3}��_{\;}^{2}+��\frac{2R}{3}��_{\;}^{2}}=\frac{2\sqrt{3}R}{3}$
$PQ=2\sqrt{{R}_{\;}^{2}-��\frac{OO��}{2}��_{\;}^{2}}=\frac{2\sqrt{6}}{3}R$
����$PQ=\frac{2\sqrt{6}}{3}\frac{m{v}_{0}^{\;}}{qB}$
��3���ڵ糡�У����ӵ�ˮƽ����λ��Ϊ$x=\frac{4}{3}\frac{m{v}_{0}^{\;}}{qB}$
���ӵ���ֱ����λ��Ϊ$y=\frac{2\sqrt{2}}{3}\frac{m{v}_{0}^{\;}}{qB}$
���˶�ѧ��ʽ��
$x=\frac{1}{2}a{t}_{\;}^{2}$
$y={v}_{0}^{\;}t$
���ӵļ��ٶ�$a=\frac{qE}{m}$
���$E=3B{v}_{0}^{\;}$
�𣺣�1��Բ�δų��İ뾶$\frac{m{v}_{0}^{\;}}{qB}$��
��2��P��Q�����ľ���$\frac{2\sqrt{2}}{3}\frac{m{v}_{0}^{\;}}{qB}$��
��3����ǿ�糡�ĵ糡ǿ�ȴ�С$3B{v}_{0}^{\;}$��
���� ���⿼���������ڴų��е��˶���������������˶����̡����������˶��켣��Ӧ��ţ�ٵڶ����ɼ�����ȷ���⣬�ɼ���֪ʶ��������˶��켣����ȷ�����ǰ����ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����ֻҪ��Ӵ����е������� | |
| B�� | ֻ��ֱ�ӽӴ���������֮��ſ��ܲ������� | |
| C�� | ѹ����֧�����ķ�����ʱ���ᴹֱ��֧���沢ָ��ѹ��֧�ֵ����� | |
| D�� | �����Ĵ�С�������ܵ������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ������Ϊm1����ΪL��ľ�����ڹ⻬��ˮƽ���ϣ�һ����Ϊm�Ļ��飨��Ϊ�ʵ㣩������ľ����ˣ�������ľ��们��Ħ�����Ĵ�СΪf����ˮƽ�ĺ㶨����F�����ڻ��飮������Ӿ�ֹ��ʼ�˶���ľ���Ҷ�ʱ��ľ���ڵ������ƶ��ľ���Ϊs�������ٶ�Ϊv1��ľ���ٶ�Ϊv2�����н�������ȷ���ǣ�������
��ͼ��ʾ������Ϊm1����ΪL��ľ�����ڹ⻬��ˮƽ���ϣ�һ����Ϊm�Ļ��飨��Ϊ�ʵ㣩������ľ����ˣ�������ľ��们��Ħ�����Ĵ�СΪf����ˮƽ�ĺ㶨����F�����ڻ��飮������Ӿ�ֹ��ʼ�˶���ľ���Ҷ�ʱ��ľ���ڵ������ƶ��ľ���Ϊs�������ٶ�Ϊv1��ľ���ٶ�Ϊv2�����н�������ȷ���ǣ�������| A�� | ����˷�Ħ���������Ĺ�Ϊf��L+s�� | |
| B�� | �����������������£�FԽ������ľ������������Խ�� | |
| C�� | ľ�������ϵ��f��L+s��=$\frac{1}{2}$m1v22 | |
| D�� | F��L+s��-fL=$\frac{1}{2}$mv12+$\frac{1}{2}$m1v22 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
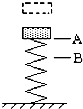 һ�����ijһ�߶��������£�����ֱ���ڵ�����ᵯ���ϣ���ͼ��ʾ����A�����忪ʼ�뵯�ɽӴ�����B��ʱ�����ٶ�Ϊ�㣬Ȼ���أ����ƿ�������������˵������ȷ���ǣ�������
һ�����ijһ�߶��������£�����ֱ���ڵ�����ᵯ���ϣ���ͼ��ʾ����A�����忪ʼ�뵯�ɽӴ�����B��ʱ�����ٶ�Ϊ�㣬Ȼ���أ����ƿ�������������˵������ȷ���ǣ�������| A�� | �����A�½���B�Ĺ����У����ܲ��ϱ�С | |
| B�� | �����B������A�Ĺ����У����ܲ��ϱ�� | |
| C�� | �����A�½���B�ʹ�B������A�Ĺ����У����ٶȶ�����������С | |
| D�� | ������AB֮��ij��ʱ��ϵͳ�����������뵯������֮����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
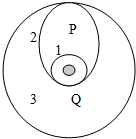 ��ͼ��ʾ���������ͬ������ʱ���Ƚ����Ƿ��䵽����Բ���1��Ȼ���ڹ����Q�㡰���ʹ��������Բ���2���У�����������Բ�����Զ�ص�Pʱ���ٴΡ���𡱣�����������ͬ��Բ���3�����Ƿֱ��ڹ��1��2��3����������ʱ��������������𡱹��̣���������ж���ȷ���ǣ�������
��ͼ��ʾ���������ͬ������ʱ���Ƚ����Ƿ��䵽����Բ���1��Ȼ���ڹ����Q�㡰���ʹ��������Բ���2���У�����������Բ�����Զ�ص�Pʱ���ٴΡ���𡱣�����������ͬ��Բ���3�����Ƿֱ��ڹ��1��2��3����������ʱ��������������𡱹��̣���������ж���ȷ���ǣ�������| A�� | �����ڹ��3������ʱ�����ʴ����ڹ��1������ʱ������ | |
| B�� | �����ڹ��3������ʱ�Ľ��ٶ�С���ڹ��1������ʱ�Ľ��ٶ� | |
| C�� | �����ڹ��1�����о���Qʱ�ļ��ٶȵ����ڹ��2�����о���P��ʱ�ļ��ٶ� | |
| D�� | �����ڹ��2�����о���Qʱ�ļ��ٶȵ����ڹ��2�����о���P��ʱ�ļ��ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
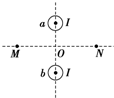 ��������ֱ����a��b����ƽ�з��ã���ͼ��ʾΪ��ֱ�ڵ��ߵĽ���ͼ����ͼ����ʾ��ƽ���ڣ�O��Ϊ�����������ߵ��е㣬M��NΪ�������߸��������㣬���������������ߵ��д����ϣ�����O��ľ�����ȣ�����������ͨ�д�С��ȡ�������ͬ�ĺ㶨����I��������߶�MN�ϸ���ĴŸ�Ӧǿ�ȵ�˵������ȷ���ǣ�������
��������ֱ����a��b����ƽ�з��ã���ͼ��ʾΪ��ֱ�ڵ��ߵĽ���ͼ����ͼ����ʾ��ƽ���ڣ�O��Ϊ�����������ߵ��е㣬M��NΪ�������߸��������㣬���������������ߵ��д����ϣ�����O��ľ�����ȣ�����������ͨ�д�С��ȡ�������ͬ�ĺ㶨����I��������߶�MN�ϸ���ĴŸ�Ӧǿ�ȵ�˵������ȷ���ǣ�������| A�� | M���N��ĴŸ�Ӧǿ�ȴ�С��ȣ�������ͬ | |
| B�� | M���N��ĴŸ�Ӧǿ�ȴ�С��ȣ������෴ | |
| C�� | ��O��ĴŸ�Ӧǿ�ȷ���ˮƽ���� | |
| D�� | ��O��ĴŸ�Ӧǿ�ȷ���ˮƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
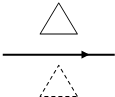 ��ͼ��ʾ��һ���պ������ε��߿�λ����ֱƽ���ڣ����·��̶�һ�����߿����ڵ���ֱƽ��ƽ���Һܿ����������ص�����ˮƽֱ���ߣ�������ͨ��ͼʾ����ĺ㶨�������߿��ʵ��λ���ɾ�ֹ�ͷţ��������˶������У�������
��ͼ��ʾ��һ���պ������ε��߿�λ����ֱƽ���ڣ����·��̶�һ�����߿����ڵ���ֱƽ��ƽ���Һܿ����������ص�����ˮƽֱ���ߣ�������ͨ��ͼʾ����ĺ㶨�������߿��ʵ��λ���ɾ�ֹ�ͷţ��������˶������У�������| A�� | �߿��ܵ��������ĺ���������ֱ���� | |
| B�� | �߿��и�Ӧ��������Ϊ��˳ʱ�����ʱ�� | |
| C�� | �߿��еĴ�ͨ��Ϊ��ʱ���Ӧ����ҲΪ�� | |
| D�� | �߿���ٵ���������ȫ��ת��Ϊ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���ٶ�a=$\frac{F}{m}$ | B�� | �Ÿ�Ӧǿ��B=$\frac{F}{IL}$ | C�� | ����C=$\frac{{?}_{r}S}{4��kd}$ | D�� | ����ǿ��I=$\frac{U}{R}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ��1���ڡ��õ��ڲⶨ���ص��������ٶȡ���ʵ���У�������˵�����̨�����С�������α꿨�ߡ��̶ȳ�֮�⣬������ѡ�õ����ģ���ȷ��һ����A��
��1���ڡ��õ��ڲⶨ���ص��������ٶȡ���ʵ���У�������˵�����̨�����С�������α꿨�ߡ��̶ȳ�֮�⣬������ѡ�õ����ģ���ȷ��һ����A���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com