
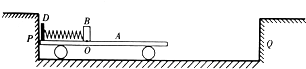
分析 (1)小车贴着P固定,对全过程研究,根据动能定理列式,可求出F.再由功能关系求弹簧的最大弹性势能Ep;
(2)撤去小车A的固定限制,B离开弹簧后,B做减速运动,A做加速运动,根据牛顿第二定律求出两者的加速度,根据速度相等的条件列式,求出时间,再由位移公式求解最小距离s0.
(3)最终A、B都停止运动,机械能转化为内能,由功能关系求B在O点右侧运动的总路程s.根据速度关系,由速度公式求出时间,再求解运动过程中B离开O点的最远距离x.
解答 解:(1)取全过程研究,根据动能定理有
Fx0-μmgx1=0
解得 F=45N
由功能关系得 Fx0=Ep
解得 Ep=45J
(2)设B运动到O点的速度为v0,根据机械能守恒定律有
Ep=$\frac{1}{2}m{v}_{0}^{2}$
接着B减速,设加速度大小为a1,根据牛顿第二定律有
μmg=ma1;
解得 a1=5m/s2;
A加速,设加速度大小为a2,根据牛顿第二定律有
μmg=Ma2;
解得 a2=2.5m/s2;
设运动的共同速度为v1,则 v1=v0-a1t1,v2=a2t1,
t1时间内A运动的距离即为最小距离 s0=$\frac{1}{2}{a}_{2}{t}_{1}^{2}$
解得 s0=0.2m
(3)最终A、B都停止运动,机械能转化为内能,由功能关系得
Ep=μmgs
解得 s=0.9m
A与Q第一次碰撞前B距离O点的距离△s1=${v}_{0}{t}_{1}-\frac{1}{2}{a}_{1}{t}_{1}^{2}-\frac{1}{2}{a}_{2}{t}_{1}^{2}$
A被Q反弹后瞬间向左速度大小为v1,B以大小为v1的速度向右减速,且B的加速度大小仍是 a1=5m/s2,方向向左;A的加速度仍为a2=2.5m/s2,方向向右,达到共同速度v2前B相对A一直向右运动,则
v12=v1-a1t2,v2=-v1+a2t2,
解得 t2=$\frac{4}{15}$s,v2=-$\frac{1}{3}$m/s
这段时间内B相对A向右移动距离△s2=(v1t2-$\frac{1}{2}{a}_{1}{t}_{2}^{2}$)-(-v1t2+$\frac{1}{2}{a}_{2}{t}_{2}^{2}$)
此时B离开O点的最远距离 x=△s1+△s2;
解得 x=0.87m
答:
(1)水平恒力F的大小是45N,弹簧的最大弹性势能Ep是45J.
(2)最初A右端与Q间的最小距离s0是0.2m.
(3)B在O点右侧运动的总路程s是0.9m,运动过程中B离开O点的最远距离x是0.87m.
点评 本题的关键理清物体的运动过程,根据牛顿第二定律和运动学公式结合分析,分析时要抓住隐含的临界条件,如速度关系.第2小题,也可以根据动量守恒定律和动能定理结合解答.


科目:高中物理 来源: 题型:解答题
 如图所示,质量为m、半径为R的小球,放在半径为2R、质量为2m的大空心球内,大球开始静止在光滑的水平面上,当小球从图示位置无初速度地沿大球内壁滚到最低点时,大球移动的距离是多少?
如图所示,质量为m、半径为R的小球,放在半径为2R、质量为2m的大空心球内,大球开始静止在光滑的水平面上,当小球从图示位置无初速度地沿大球内壁滚到最低点时,大球移动的距离是多少?查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在圆轨道上运行的空间站里,一宇航员A静止(相对空间舱)“站”在舱内朝向地球一侧的“地面”B上,则下列说法正确的是( )
如图所示,在圆轨道上运行的空间站里,一宇航员A静止(相对空间舱)“站”在舱内朝向地球一侧的“地面”B上,则下列说法正确的是( )| A. | 若宇航员A将手中小球无初速(相对空间舱)释放,该球将落到“地面”B上 | |
| B. | 宇航员A所受重力与他在该位罝所受的万有引力相等 | |
| C. | 宇航员A与“地面”B之间无弹力作用 | |
| D. | 宇航员A不受重力作用 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
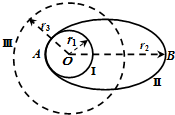 地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )
地球质量为M,半径为R,自转周期为T0,取无穷远处的引力势能为零.质量为m的卫星在绕地球无动力飞行时,它和地球组成的系统机械能守恒,它们之间引力势能的表达式是Ep=-$\frac{GMm}{r}$,其中r是卫星与地心间的距离.现欲将质量为m的卫星从近地圆轨道Ⅰ发射到椭圆轨道Ⅱ上去,轨道Ⅱ的近地点A和远地点B距地心分别为r1=R,r2=3R.若卫星在轨道Ⅱ上的机械能和在r3=2R的圆周轨道Ⅲ上的机械能相同,则( )| A. | 卫星在近地圆轨道Ⅰ上运行的周期与地球自转周期相同 | |
| B. | 从轨道Ⅰ发射到轨道Ⅱ需要在近地的A点一次性给它提供能量$\frac{GMm}{4R}$ | |
| C. | 卫星在椭圆轨道上的周期为T0$\sqrt{(\frac{{r}_{2}+R}{R})^{3}}$ | |
| D. | 卫星在椭圆轨道Ⅱ上自由运行时,它在B点的机械能大于在A点的机械能 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 卢瑟福通过α粒子散射实验证实了原子内部有一个体积很小的原子核 | |
| B. | 铀核(${\;}_{92}^{238}$U)衰变为铅核(${\;}_{82}^{206}$Pb)的过程中,要经过6次α衰变和8次β衰变 | |
| C. | 按照爱因斯坦的理论,在光电效应中,金属中的电子吸收一个光子获得的能量是hv,这些能量的一部分用来克服金属的逸出功W0,剩下的表现为逸出后电子的初动能Ek | |
| D. | 玻尔的原子理论第一次将量子观念引入原子领域,提出了定态和跃迁的概念,成功地解释了所有原子光谱的实验规律. | |
| E. | 铀核(${\;}_{92}^{238}$U)衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于铀核的结合能 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
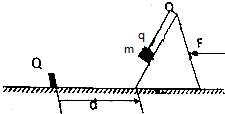 如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求:
如图所示,在粗糙水平面上有一质量为M=2kg的粗糙斜面体、斜面的倾角θ=30°,在斜面体的左侧相距为d=1.5m处有一固定障碍物Q,将一质量为m=0.2kg的小物块(可视为质点)用绝缘绳系住,绳的一端固定在斜面体的顶端,此时小物块恰好能在斜面体上与斜面体一起保持静止且绳刚好伸直无弹力.现给斜面体施加一水平向左的推力F,使斜面体和小物块一起向左做匀加速运动,当斜面体到达障碍物Q与其碰撞后,斜面体立即被障碍物Q锁定.已知斜面体与地面间的动摩擦因数为μ1=0.5,重力加速度g=10m/s2,设滑动摩擦力等于最大静摩擦力,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在x轴上方有垂直于xoy平面向里的匀强磁场,磁感应强度为B;在x轴下方有一沿y轴负方向的匀强电场,场强为E,一质量为m,电量为-q的粒子从坐标原点O沿y轴负向射出,经过一段时间粒子到达x轴上的A点,A点与点O的距离为L.若不计重力.求
如图所示,在x轴上方有垂直于xoy平面向里的匀强磁场,磁感应强度为B;在x轴下方有一沿y轴负方向的匀强电场,场强为E,一质量为m,电量为-q的粒子从坐标原点O沿y轴负向射出,经过一段时间粒子到达x轴上的A点,A点与点O的距离为L.若不计重力.求查看答案和解析>>
科目:高中物理 来源: 题型:计算题
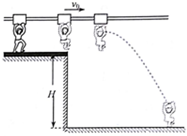 某电视娱乐节目“快乐向前冲”的场地设施如图.足够长的水平滑杆上装有可沿杆自由滑动的悬挂器,悬挂器与滑杆的动摩擦因数为μ=0.2,选手在离地高H=5m的平台上,抓住悬挂器经过一定距离的助跑,可获得初速度并滑离平台.为了落在地面合适的位置,选手必须做好判断,在合适的时机位置放开悬挂器,g取10m/s2.
某电视娱乐节目“快乐向前冲”的场地设施如图.足够长的水平滑杆上装有可沿杆自由滑动的悬挂器,悬挂器与滑杆的动摩擦因数为μ=0.2,选手在离地高H=5m的平台上,抓住悬挂器经过一定距离的助跑,可获得初速度并滑离平台.为了落在地面合适的位置,选手必须做好判断,在合适的时机位置放开悬挂器,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求:
一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com