
 如图所示,在平面直角坐标系xOy中的第Ⅰ象限内存在以两坐标轴为边界、沿x轴负方向的匀强电场;在第Ⅱ象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界圆形匀强磁场区域(图中未画出).一质子从坐标为(l,0)的M点以速度v0垂直x轴进入第Ⅰ象限,恰好能通过y轴上坐标为(0,2l)的N点进入第Ⅱ象限,质子在第Ⅱ象限内通过磁场后速度方向恰好与射线OP垂直,已知质子的质量为mH,电荷量为e,不计质子的重力,射线OP在第Ⅱ象限内与x轴负方向成30°角.求:
如图所示,在平面直角坐标系xOy中的第Ⅰ象限内存在以两坐标轴为边界、沿x轴负方向的匀强电场;在第Ⅱ象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界圆形匀强磁场区域(图中未画出).一质子从坐标为(l,0)的M点以速度v0垂直x轴进入第Ⅰ象限,恰好能通过y轴上坐标为(0,2l)的N点进入第Ⅱ象限,质子在第Ⅱ象限内通过磁场后速度方向恰好与射线OP垂直,已知质子的质量为mH,电荷量为e,不计质子的重力,射线OP在第Ⅱ象限内与x轴负方向成30°角.求:分析 (1)质子在电场中做类似平抛运动,x方向匀速,y方向匀加速,根据运动学公式列式求解;
(2)先根据运动学公式列式求解出x、y方向的分速度,然后根据几何关系列式求解;
(3)先根据洛伦兹力提供向心力求解出轨迹的半径,然后求得磁场的最小半径,再求出最小面积.
解答 解:(1)质子刚进入第Ⅰ象限运动时,受到水平向左的电场力,
具有竖直向上的初速度,故质子做类平抛运动,有:
水平方向:eE=mHa,l=$\frac{1}{2}$at2,
竖直方向:2l=v0t,
解得:E=$\frac{m{v}_{0}^{2}}{2el}$.
(2)设质子到达N点的速度大小为vN,方向与y轴正方向的夹角为θ,
质子做类平抛运动,有:
水平方向:l=$\frac{{v}_{x}}{2}$t,
竖直方向:2l=v0t,
根据几何关系有:tanθ=$\frac{{v}_{x}}{{v}_{0}}$,
解得:vx=v0,tanθ=1,θ=45°.
(3)质子在第Ⅱ象限内的轨迹如图所示:
质子到达N点时的速度:vN=$\sqrt{{v}_{0}^{2}+{v}_{x}^{2}}$=$\sqrt{2}$v0,
当质子在磁场中做匀速圆周运动时,由牛顿第二定律有:evNB=mH$\frac{{v}_{N}^{2}}{r}$,
由几何关系可知,质子在磁场中偏转105°后垂直于OP射出,
四边形O1N'AQ为正方形,则以QN连线为直径的圆对应的面积就是圆形磁场区域的最小面积,
磁场区域的最小半径:R=rsin$\frac{105°}{2}$,
故磁场的最小面积为S=πR2,
解得:S=$\frac{2π{m}_{H}^{2}{v}_{0}^{2}(sin52.5°)^{2}}{{e}^{2}{B}^{2}}$.
答:(1)匀强电场的电场强度E的大小为$\frac{m{v}_{0}^{2}}{2el}$.
(2)电子离开第Ⅰ象限时的速度方向与y轴正方向的夹角θ为45°.
(3)该圆形磁场区域的最小面积为$\frac{2π{m}_{H}^{2}{v}_{0}^{2}(sin52.5°)^{2}}{{e}^{2}{B}^{2}}$.
点评 本题中粒子先在电场中做类似平抛运动,然后进入磁场做匀速圆周运动,要注意两个轨迹的连接点,然后根据运动学公式和牛顿第二定律以及几何关系列式求解,其中画出轨迹是关键.


科目:高中物理 来源: 题型:解答题
 在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上自纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=l0.00cm,A、B间的距离y1=5.02cm,B、C间的距离y2=14.82cm.
在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上自纸和复写纸.将该木板竖直立于水平地面上,使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口方向平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口方向平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=l0.00cm,A、B间的距离y1=5.02cm,B、C间的距离y2=14.82cm.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
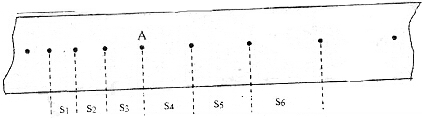 如图所示,某同学在做“研究匀变速直线运动”试验中,由打点计时器得到表示小车运动的一条纸带,纸带上相邻计数点的时间间隔为T=0.10s,各间距S1=7.05cm,S2=7.687cm,S3=8.33cm,S4=8.95cm,S5=9.61cm,S6=10.26cm,则A处瞬时速度的大小为0.864,小车运动加速度的表达式为$\frac{({s}_{4}+{s}_{5}+{s}_{6})-({s}_{1}+{s}_{2}+{s}_{3})}{9{T}^{2}}$,加速度的大小为0.639.(以上计算结果均保留三位有效数字)
如图所示,某同学在做“研究匀变速直线运动”试验中,由打点计时器得到表示小车运动的一条纸带,纸带上相邻计数点的时间间隔为T=0.10s,各间距S1=7.05cm,S2=7.687cm,S3=8.33cm,S4=8.95cm,S5=9.61cm,S6=10.26cm,则A处瞬时速度的大小为0.864,小车运动加速度的表达式为$\frac{({s}_{4}+{s}_{5}+{s}_{6})-({s}_{1}+{s}_{2}+{s}_{3})}{9{T}^{2}}$,加速度的大小为0.639.(以上计算结果均保留三位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压75mmHg.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?
如图所示,竖直放置的U形管,左端封闭右端开口,管内水银将长19cm的空气柱封在左管内,此时两管内水银面的高度差为4cm,大气压强为标准大气压75mmHg.现向右管内再注入水银,使空气柱长度减少1cm,若温度保持不变,则需注入水银柱的长度为多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,某次发生山洪泥石流灾害时,有一辆汽车停在小山坡底,司机发现在距坡底224m的山坡处泥石流正以10m/s的初速度、0.5m/s2的加速度匀加速倾泻而下,假设司机(反应时间为1s)以0.3m/s2的加速度匀加速启动汽车且一直做匀加速直线运动,而泥石流到达坡底后速率不变且在水平面的运动近似看成匀速直线运动.
如图所示,某次发生山洪泥石流灾害时,有一辆汽车停在小山坡底,司机发现在距坡底224m的山坡处泥石流正以10m/s的初速度、0.5m/s2的加速度匀加速倾泻而下,假设司机(反应时间为1s)以0.3m/s2的加速度匀加速启动汽车且一直做匀加速直线运动,而泥石流到达坡底后速率不变且在水平面的运动近似看成匀速直线运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com