
(14分)
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
【解析】:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算对)
23.【题文】(16分)
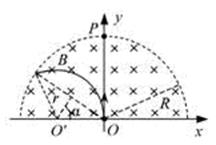
 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经![]() 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
(1)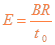 (2)
(2)![]() (3)
(3)![]()
解析::(1)设带电粒子的质量为m,电荷量为q,初速度为v,电场强度为E。可判断出粒子受到的洛伦磁力沿x轴负方向,于是可知电场强度沿x轴正方向
且有 qE=qvB ①
又 R=vt0 ②
则 ![]() ③
③
(2)仅有电场时,带电粒子在匀强电场中作类平抛运动
在y方向位移 ![]() ④
④
由②④式得 ![]() ⑤
⑤
设在水平方向位移为x,因射出位置在半圆形区域边界上,于是
![]()
又有 ![]() ⑥
⑥
得 ![]() ⑦
⑦
 (3)仅有磁场时,入射速度
(3)仅有磁场时,入射速度![]() ,带电粒子在匀强磁场中作匀速圆周运动,设轨道半径为r,由牛顿第二定律有
,带电粒子在匀强磁场中作匀速圆周运动,设轨道半径为r,由牛顿第二定律有
![]() ⑧
⑧
又 qE=ma ⑨
由⑦⑧⑨式得 ![]() ⑩
⑩
由几何关系 ![]() 11
11
即 ![]()
![]() 12
12
带电粒子在磁场中运动周期
![]()
则带电粒子在磁场中运动时间
![]()
所以 ![]() 13
13


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中物理 来源: 题型:
| a3 | T2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
| a3 | T2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
查看答案和解析>>
科目:高中物理 来源: 题型:
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
查看答案和解析>>
科目:高中物理 来源:2011-2012学年江西省赣州市十一县(市)高一下学期期中联考物理试题(解析版) 题型:计算题
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即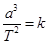 ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质量M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com