
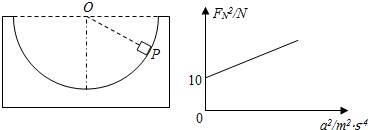
分析 (1)对滑块受力分析,由牛顿第二定律求出加速度,然后答题.
(2)由图象求出压力与加速度,应用牛顿第二定律求出滑块质量.
解答 解:(1)对滑块,由牛顿第二定律得:mgcotθ=ma,解得:a=gcotθ,加速度方向水平向左,容器可能向左做加速运动,或向右做减速运动.
(2)由图示图象可知,FN=10N,a=0,
此时滑块位移容器底部,处于平衡状态,
由平衡条件得:FN=mg,解得:m=1kg,
块,由牛顿第二定律得:mgcotθ=ma,mg=$\frac{ma}{cotθ}$,
对滑块,FN=$\frac{mg}{sinθ}$=$\frac{ma}{cosθ}$=$\frac{m}{cosθ}$a,则图象的斜率:k=$\frac{m}{cosθ}$;
答:(1)容器的加速度为:gcotθ,加速度方向水平向左,容器可能向左做加速运动,或向右做减速运动.
(2)滑块质量为1kg,图象的斜率为$\frac{m}{cosθ}$.
点评 本题考查了求加速度、质量问题,应用牛顿第二定律即可正确解题.


科目:高中物理 来源: 题型:选择题
| A. | 行星绕恒星运动轨迹为圆形,则它运动的周期平方与轨道半径的三次方之比k为常数,此常数的大小与恒星的质量和行星的速度有关 | |
| B. | 匀速圆周运动是速度大小不变的匀变速曲线运动,速度方向始终为运动轨迹该点的切线方向 | |
| C. | 牛顿发现的万有引力定律,卡文迪许用实验方法测出万有引力恒量的数值,从而使万有引力定律有了真正的实用价值 | |
| D. | 奥斯特发现了电与磁间的关系,即电流的周围存在着磁场;同时他通过实验发现了磁也能产生电,即电磁感应现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,PQ、MN为两条固定的光滑平行金属导轨,间距L=2m,导轨电阻忽略不计,两导轨处在同一水平面上.导轨上放有两根电阻均为r=1Ω、质量均为m=0.2Kg且与导轨垂直的金属杆ab、cd,导轨中间的区域有磁感应强B=0.5T、方向竖直向上的匀强磁场.金属杆cd系一轻质细绳,跨过轻质定滑轮与地面上质量为M=1Kg的物体相连.不计摩擦,开始时两金属杆均处于静止状态,细绳绷直但没有拉力.t=0时,给金属杆ab施加一个水平拉力F,使ab以加速度a=2m/s2向左做匀加速运动.求:
如图所示,PQ、MN为两条固定的光滑平行金属导轨,间距L=2m,导轨电阻忽略不计,两导轨处在同一水平面上.导轨上放有两根电阻均为r=1Ω、质量均为m=0.2Kg且与导轨垂直的金属杆ab、cd,导轨中间的区域有磁感应强B=0.5T、方向竖直向上的匀强磁场.金属杆cd系一轻质细绳,跨过轻质定滑轮与地面上质量为M=1Kg的物体相连.不计摩擦,开始时两金属杆均处于静止状态,细绳绷直但没有拉力.t=0时,给金属杆ab施加一个水平拉力F,使ab以加速度a=2m/s2向左做匀加速运动.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
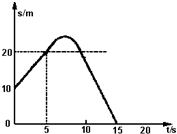
| A. | 0-5s内物体做匀速直线运动 | |
| B. | 10-15s内物体做匀减速直线运动 | |
| C. | 10-15s内物体做匀速直线运动,速度的方向与0-5s内的方向相反 | |
| D. | 物体在0-15s内的位移为10m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 加速前进时,马向前拉车的力大于车向后拉马的力 | |
| B. | 只有匀速前进时,马向前拉车和车向后拉马的力大小相等 | |
| C. | 无论加速或匀速前进,马向前拉车与车向后拉马的力大小都是相等的 | |
| D. | 车或马是匀速前进还是加速前进,取决于马拉车和车拉马这一对力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 点电荷就是元电荷 | |
| B. | 根据F=k$\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}$知,当两电荷间的距离趋近于零时,库仑力将趋近于无穷大 | |
| C. | 若两点电荷的电量Q1>Q2,则Q1对Q2的库仑力大于Q2对Q1的库仑力 | |
| D. | 静电力常量的数值是由实验得到的 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 已知圆形电流在过圆心的中心轴线上产生的磁感应强度为B=$\frac{μI{R}^{2}}{2({R}^{2}+{Z}^{2})\frac{3}{2}}$其中I表示电流强度强度,R表示圆的半径,μ是常数,Z为中心轴线上任意一点到O1或O2的距离,现有两个图形线圈,如图乙所示,半径均为R,平行地共轴位置,两圆心O1、O2相距为a,所截电流均为I,且电流方向相同,以连的磁感应强度大小的表达式为( )
已知圆形电流在过圆心的中心轴线上产生的磁感应强度为B=$\frac{μI{R}^{2}}{2({R}^{2}+{Z}^{2})\frac{3}{2}}$其中I表示电流强度强度,R表示圆的半径,μ是常数,Z为中心轴线上任意一点到O1或O2的距离,现有两个图形线圈,如图乙所示,半径均为R,平行地共轴位置,两圆心O1、O2相距为a,所截电流均为I,且电流方向相同,以连的磁感应强度大小的表达式为( )| A. | B=$\frac{μI{R}^{2}}{2}${$\frac{1}{{[R}^{2}+(a+x)^{2}]^{\frac{3}{2}}}$+$\frac{1}{[{R}^{2}+(a-x)^{2}]^{\frac{3}{2}}}$} | |
| B. | B=$\frac{μI{R}^{2}}{2}${$\frac{1}{{[R}^{2}+(\frac{a}{2}+x)^{2}]^{\frac{3}{2}}}$-$\frac{1}{[{R}^{2}+(\frac{a}{2}-x)^{2}]^{\frac{3}{2}}}$} | |
| C. | B=$\frac{μI{R}^{2}}{2}${$\frac{1}{{[R}^{2}+(\frac{a}{2}+x)^{2}]^{\frac{3}{2}}}$+$\frac{1}{[{R}^{2}+(\frac{a}{2}-x)^{2}]^{\frac{3}{2}}}$} | |
| D. | B=$\frac{μI{R}^{2}}{2}${$\frac{x}{[{R}^{2}+(\frac{a}{2}+x)^{2}]^{\frac{3}{2}}}$+$\frac{x}{[{R}^{2}+(\frac{a}{2}-x)^{2}]^{\frac{3}{2}}}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com