
分析 (1)B车做匀减速直线运动,已知刹车距离,根据速度位移关系公式求解刹车的加速度;
(2)两车能够相撞或者最近距离的临界情况是两车速度相等,先根据速度时间关系公式求解速度相同的时间,然后分别求解出两车的位移进行判断.
解答 解:(1)B车刹车至停下来过程中,由v2-v02=2ax,
得:aB=$\frac{{v}^{2}-{v}_{0}^{2}}{2x}$=$\frac{0-3{0}^{2}}{2×180}$=-2.5m/s2;
(2)假设不相撞,设经过时间t两车速度相等,对B车有:vA=vB+aBt
解得:t=$\frac{{v}_{A}-{v}_{B}}{{a}_{B}}$=$\frac{10-30}{-2.5}$=8s,
此时,B车的位移有:xB=vBt+$\frac{1}{2}$aBt2=30×8-$\frac{1}{2}$=160m,
A车位移有:xA=vAt=80m,
因xB<x0+xA故两车不会相撞,两车最近距离为:△x=5m
答:(1)B车刹车时的加速度是-2.5m/s2.
(2)乙车能避免和甲车相撞.
点评 本题考查了匀变速直线运动规律的应用问题,对于追击问题,关键抓住一个临界条件(速度相同)和两个等量关系(位移关系和时间关系).


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中物理 来源: 题型:多选题
 如图所示,轻质弹簧上端固定在天花板上,下端拴一小球.小球在重力和弹簧弹力的作用下沿竖直方向不停地往复运动,不计空气阻力,下列说法中正确的是( )
如图所示,轻质弹簧上端固定在天花板上,下端拴一小球.小球在重力和弹簧弹力的作用下沿竖直方向不停地往复运动,不计空气阻力,下列说法中正确的是( )| A. | 小球的机械能守恒 | |
| B. | 小球与弹簧组成的系统机械能守恒 | |
| C. | 弹簧处于原长时,小球的机械能最小 | |
| D. | 弹簧处于最长时,小球的机械能最小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
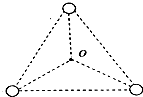 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )| A. | 每个星体受到向心力大小均为3$\frac{G{m}^{2}}{{a}^{2}}$ | |
| B. | 每个星体的角速度均为$\sqrt{\frac{3Gm}{{a}^{2}}}$ | |
| C. | 若a不变,m是原来的两倍,则周期是原来的$\frac{1}{2}$ | |
| D. | 若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做直线运动 | B. | 做曲线运动 | ||
| C. | 可能做匀速圆周运动 | D. | 运动速度大小一定不断增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不等的小球.按下述步骤做实验:
为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞,某同学选取了两个体积相同、质量不等的小球.按下述步骤做实验:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求:
如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
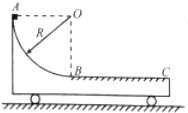 如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求:
如图所示,质量为M=2kg的小车静止在光滑的水平地面上,其AB部分为半径R=0.5m的光滑$\frac{1}{4}$圆弧,BC部分水平粗糙,BC长为L=1m,一质量m=1kg可看做质点的小物块从A点由静止释放,恰好能滑到C点,重力加速度取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com