
| A�� | ���������ĺ�������Ϊ�� | |
| B�� | F1��F2�������ĺ�����С����Ϊ20N | |
| C�� | �����崦������ֱ���˶�״̬����F1��F3�ĺ�����СΪ48N������ָ������ | |
| D�� | �����崦�ھ�ֹ״̬����F1��F3�ĺ�����Сһ��Ϊ28N������ָ������ |
���� ������F1��F2�ĺ����ķ�ΧΪ��|F1-F2|��F��F1+F2��
���������ܹ�����F1��F2��F3���ã�������ķ���������ģ�����һ�����Ĵ�С�������������ĺ�����Χ֮�ڣ���ô��������������СֵΪ��
��� �⣺A������������F1��F2�ĺ�����Χ|F1-F2|��F����F1+F2����F1��F2�ĺ�����ΧΪ14N��F����70N��F3=20N����F3��F1��F2�ĺ�����С������ȣ����������ĺ�������Ϊ�㣮��A��ȷ��
B��F1��F2�ĺ�����ΧΪ14N��F����70N����F1��F2�������ĺ�����С����Ϊ20 N����B��ȷ��
C�������崦������ֱ���˶�״̬��������Ϊ�㣬F1��F3�ĺ�����F2=28N��С��ȡ������෴����F1��F3�ĺ�����СΪ28N��������F2�����෴�����ϣ���C����
D�������崦�ھ�ֹ״̬��������Ϊ�㣬F1��F3�ĺ�����С��F2=28N��С��ȣ������෴����F1��F3�ĺ�����Сһ��Ϊ28 N������ָ�����ϣ���D��ȷ��
��ѡ��ABD
���� ����ؼ�Ҫ��ȷ�����������ĺ����ķ�Χ��ͬʱҪ��ȷ����ƽ��ʱ�������������ĺ��������������ֵ�������ߣ��ѶȲ������ڻ����⣮


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��x����ˮƽ����y������ֱ����OM����x��ɦȽǵ�һ�����ߣ��ִ�����ԭ��O���ٶ�v0ˮƽ�׳�һ��С��С��������OM����P�㣬��ʱС����ٶ�v��OM�ļн�Ϊa�������ַ������С���������Ϊ2vo��С��������OM����P�䣬��ʱС����ٶ�v����OM�ļн�Ϊa�䣬������
��ͼ��ʾ��x����ˮƽ����y������ֱ����OM����x��ɦȽǵ�һ�����ߣ��ִ�����ԭ��O���ٶ�v0ˮƽ�׳�һ��С��С��������OM����P�㣬��ʱС����ٶ�v��OM�ļн�Ϊa�������ַ������С���������Ϊ2vo��С��������OM����P�䣬��ʱС����ٶ�v����OM�ļн�Ϊa�䣬������| A�� | С���O�˶���P���ʱ���Ǵ�O��Pʱ���2�� | |
| B�� | �н�a����a��2�� | |
| C�� | С��ͨ��P����������4v | |
| D�� | OP��=2OP |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼΪ̽��ƽ�а�������ĵ�������Щ�����йص�ʵ�飮
��ͼΪ̽��ƽ�а�������ĵ�������Щ�����йص�ʵ�飮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | E${\;}_{{v}_{2}}$��E${\;}_{{v}_{1}}$��T2��T1 | B�� | E${\;}_{{v}_{2}}$��E${\;}_{{v}_{1}}$��T2��T1 | ||
| C�� | E${\;}_{{v}_{2}}$��E${\;}_{{v}_{1}}$��T2��T1 | D�� | E${\;}_{{v}_{2}}$��E${\;}_{{v}_{1}}$��T2��T1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �ռ���P��Q���㴦���̶�һ�����ɣ�����P�㴦Ϊ����ɣ�P��Q���㸽���糡�ĵ�����ֲ���ͼ��ʾ��a��b��c��dΪ�糡�е�4���㣮������
�ռ���P��Q���㴦���̶�һ�����ɣ�����P�㴦Ϊ����ɣ�P��Q���㸽���糡�ĵ�����ֲ���ͼ��ʾ��a��b��c��dΪ�糡�е�4���㣮������| A�� | Q�����õ�ҲΪ����� | |
| B�� | a���b��ĵ糡ǿ����ͬ | |
| C�� | ͬһ�������c��ĵ�����С����d��ĵ����� | |
| D�� | ����ɴ�a���Ƶ�c������ܼ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �ڵ糡ǿ��ΪE=104N/C������ˮƽ���ҵ���ǿ�糡�У���һ����l=1m�ľ�Եϸ�ˣ��������ƣ��̶�һ������Ϊm=0.2kg�ĵ���Ϊq=5��10-5C�������С��ϸ�˿�����O����ֱƽ��������ת�����ֽ��˴�ˮƽλ��A�����ͷţ���С���˶�����͵�B��ʱ�˵��������ȡg=10m/s2��
�ڵ糡ǿ��ΪE=104N/C������ˮƽ���ҵ���ǿ�糡�У���һ����l=1m�ľ�Եϸ�ˣ��������ƣ��̶�һ������Ϊm=0.2kg�ĵ���Ϊq=5��10-5C�������С��ϸ�˿�����O����ֱƽ��������ת�����ֽ��˴�ˮƽλ��A�����ͷţ���С���˶�����͵�B��ʱ�˵��������ȡg=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
| ����� | A | C | C | B | A | B |
| �ڱ��� | C | A | B | C | B | A |
| �� ֵ | ����ֵ | ��ֵͬAC��ֵ | �ܴ� | ��С | �ܴ� | �ӽ�AC����ֵ |

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
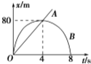
| A�� | A��B���ʵ���4sĩ���� | |
| B�� | B�ʵ����4s�������˶�����4���������˶� | |
| C�� | B�ʵ�������������ֱ���˶������ظ�������ֱ���˶� | |
| D�� | A�ʵ���20m/s���ٶ������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{{{m_2}{R_1}}}{{{m_1}{R_2}}}}$v��$\sqrt{\frac{{{m_1}R_2^3}}{{{m_2}R_1^3}}}$T | |
| B�� | $\sqrt{\frac{{{m_1}{R_2}}}{{{m_2}{R_1}}}}$v��$\sqrt{\frac{{{m_2}R_1^3}}{{{m_1}R_2^3}}}$T | |
| C�� | $\sqrt{\frac{{{m_2}{R_1}}}{{{m_1}{R_2}}}}$v��$\sqrt{\frac{{{m_2}R_1^3}}{{{m_1}R_2^3}}}$T | |
| D�� | $\sqrt{\frac{{{m_1}{R_2}}}{{{m_2}{R_1}}}}$v��$\sqrt{\frac{{{m_1}R_2^3}}{{{m_2}R_1^3}}}$T |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com