
科目:高中物理 来源: 题型:021
如图所示,两颗靠得很近的恒星称为双星,这两颗星必须各以一定速率绕某一中心O匀速转动才不至于因万有引力作用而吸引在一起,那么
[ ]
A.它们做圆周运动的角速度与其质量成反比
B.它们做圆周运动的线速度与其质量成反比
C.它们做圆周运动的半径与其质量成反比
D.它们所受向心力与其质量成反比
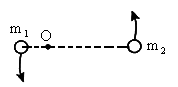
查看答案和解析>>
科目:高中物理 来源:物理教研室 题型:038
两颗靠得很近的恒星称为双星,这两颗星必须以一定角速度绕二者连线上的某一点转动才不至于由于万有引力的作用而吸引到一起.已知两颗星的质量分别为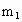 、
、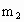 ,相距为L,试求:(1)两颗星转动中心的位置;
,相距为L,试求:(1)两颗星转动中心的位置;
(2)这两颗星转动的周期.
查看答案和解析>>
科目:高中物理 来源: 题型:038
如图所示,两颗靠得很近的恒星称为双星,这两颗星必须各以一定速率绕某一中心转动才不致于因万有引力作用而吸引在一起.已知双星的质量分别为m1和m2,相距为L,万有引力常数为G.求:
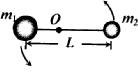
①双星转动中心位置O与m1的距离;
②转动周期
查看答案和解析>>
科目:高中物理 来源:物理教研室 题型:038
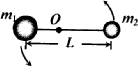
①双星转动中心位置O与m1的距离;
②转动周期
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com