
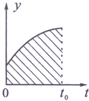
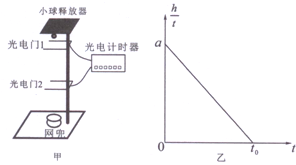
 Ԫ�ۻ����dz��õ������о���������ͼ��ʾΪij��������ʱ��仯�ĺ���ͼ���ڴ�ͼ������������Χ��������������壬����˵����ȷ���ǣ�������
Ԫ�ۻ����dz��õ������о���������ͼ��ʾΪij��������ʱ��仯�ĺ���ͼ���ڴ�ͼ������������Χ��������������壬����˵����ȷ���ǣ�������| A�� | ���y��ʾ���ٶȣ�����������ʵ�t0��ʱ�̵��ٶ� | |
| B�� | ���y��ʾ�����õ����ĵ������������������Ӧʱ���ڸ��õ������ĵĵ��� | |
| C�� | ���y��ʾ�������Ĺ��ʣ���������ڸ�������Ӧʱ���������Ĺ� | |
| D�� | ���y��ʾ�仯�ų��ڽ�����Ȧ�в����ĵ綯�ƣ���������ڸôų�����Ӧʱ���ڴŸ�Ӧǿ�ȵı仯�� |
���� �������ͼ���������ʾ�������ں����������������������ij˻���������ֵ�������صĹ��ɽ��з�����
��� �⣺A�����y���ʾ���ٶȣ���a=$\frac{��v}{��t}$֪����v=a��t��֪��������ʵ�����Ӧʱ���ڵ��ٶȱ仯�������ٶȣ���A����
B�����y���ʾ�������ĵ�������q=It��֪������ڸ�������Ӧʱ����ͨ���õ����ĵ�������B����
C�����y��ʾ�������Ĺ��ʣ���������ڸ�������Ӧʱ���������Ĺ�����C��ȷ
D�����y���ʾ�仯�ų��ڽ�����Ȧ�����ĵ綯�ƣ�����E=$\frac{����}{��t}$֪������=E•��t֪��������ڸôų�����Ӧʱ���ڴ�ͨ���ı仯�������ǴŸ�Ӧǿ�ȵı仯������D����
��ѡ��C��
���� ���⿼��ͼ����������壬Ҫѧ���ͨ���ܾ�һ�������ؼ�Ҫ������ص��������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
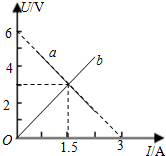 ��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A��
��ͼ��ʾ��a��ij��Դ��U?Iͼ�ߣ�b�ǵ���R��U?Iͼ�ߣ���ͼ��֪�����Դ�ĵ綯�Ƶ���6V������������Դ���������R�����ɱպϵ�·����ñպϻ�·�ĵ�����С����1.5A���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{n}{k}}$T | B�� | $\sqrt{\frac{{n}^{2}}{k}}$T | C�� | $\sqrt{\frac{{n}^{3}}{{k}^{2}}}$T | D�� | $\sqrt{\frac{{n}^{3}}{k}}$T |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
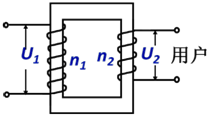 ij�ͺű�ѹ��ԭ����Ȧ������Ϊn1��n2=5��1�����Ӹ�ѹ�߱�ѹ���������ͼ������ȷ���ǣ�������
ij�ͺű�ѹ��ԭ����Ȧ������Ϊn1��n2=5��1�����Ӹ�ѹ�߱�ѹ���������ͼ������ȷ���ǣ�������| A�� | һ���ͥ��·�ĵ�ѹΪU2=220$\sqrt{2}$V | |
| B�� | ���ѧУʵ����Ҳ�����û������磬�����ʱ����ʱ����Ϊ0.02s | |
| C�� | ��ѹ������Ľ�����Ƶ��Ϊ250Hz | |
| D�� | �ö��ñ�����U1ԼΪ1100V |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ������M=3kg��С��A��ֹ��ˮƽ���ϣ�С������һ����m=1kg��С���B����һ���ʵ���ѹ������������ʱ���ɵĵ�������ΪEp=6J��С�����С���ұھ���Ϊl=0.4m�����������С������뵯�ɺ���С���ұڷ�����ײ����ײ������е����ʧ������һ��Ħ������
��ͼ��ʾ��һ������M=3kg��С��A��ֹ��ˮƽ���ϣ�С������һ����m=1kg��С���B����һ���ʵ���ѹ������������ʱ���ɵĵ�������ΪEp=6J��С�����С���ұھ���Ϊl=0.4m�����������С������뵯�ɺ���С���ұڷ�����ײ����ײ������е����ʧ������һ��Ħ�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ����ʿ������ʱʹ�ñ㲽����Ϊ�˷�ֹ�ŷ����������� | |
| B�� | ��е���͵�Ų��ڽ����еĴ����ٶȽ��ɽ��ʾ��� | |
| C�� | ���������ǹ�ͨ��Բ��������ʱ�γɵ� | |
| D�� | ���㲣�������ڵ���Ʒʱ���ھ�ͷǰ��װһ��ƫ��Ƭ�Լ��������ķ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
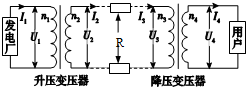 Զ��������ԭ��ͼ��ͼ��ʾ������ѹ��ѹ��ԭ����Ȧ����������ѹ����������·������ͼ����ѹ��Ϊ�����ѹ���������й�ϵʽ��ȷ���ǣ�������
Զ��������ԭ��ͼ��ͼ��ʾ������ѹ��ѹ��ԭ����Ȧ����������ѹ����������·������ͼ����ѹ��Ϊ�����ѹ���������й�ϵʽ��ȷ���ǣ�������| A�� | $\frac{{I}_{1}}{{I}_{2}}$=$\frac{{n}_{1}}{{n}_{2}}$ | B�� | I2=$\frac{{U}^{2}}{R}$ | ||
| C�� | I1U1=I2U2 | D�� | ��n2���ӣ��û��õ��ĵ�ѹ���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com