
 ��ͼ��ʾ�������ƽ�еļ�����״��ȫ��ͬ������ƽ�н�����a��b��c��d���İ崹ֱ��ֽ����ã��İ峤��ΪL�����������ľ���ҲΪL�����Ȳ��ƣ�a��b����c��d������ͬ��С����ǿ�糡�����������糡�������Ҳ�����I���������II ���д�ֱ��ֽ�����ǿ�ų���ͼ��δ������������һ����Ϊm������Ϊq�������Ӵ�a��b �������е�O�ؼ����������Գ��ٶ�v����ƽ�н�����a��b��䣬ǡ�ô�a���Ҳ��Ե�����Ӵ����ɳ�����ų�����I�����ǡ�ܴ�d���Ҳ��Ե�����Ӵ�������c��d�䲢�� c��d������е�O���ؼ��������߽���ų������Ȼ��պûص�a��b�����O�����������˶���������������������
��ͼ��ʾ�������ƽ�еļ�����״��ȫ��ͬ������ƽ�н�����a��b��c��d���İ崹ֱ��ֽ����ã��İ峤��ΪL�����������ľ���ҲΪL�����Ȳ��ƣ�a��b����c��d������ͬ��С����ǿ�糡�����������糡�������Ҳ�����I���������II ���д�ֱ��ֽ�����ǿ�ų���ͼ��δ������������һ����Ϊm������Ϊq�������Ӵ�a��b �������е�O�ؼ����������Գ��ٶ�v����ƽ�н�����a��b��䣬ǡ�ô�a���Ҳ��Ե�����Ӵ����ɳ�����ų�����I�����ǡ�ܴ�d���Ҳ��Ե�����Ӵ�������c��d�䲢�� c��d������е�O���ؼ��������߽���ų������Ȼ��պûص�a��b�����O�����������˶������������������������� ��1�������ڵ糡������ƽ���˶��������ӵ��˶��ֽ⣬���������������糡ʱ���ٶȴ�С��Ȼ���϶��ܶ�����������糡ǿ�ȵĴ�С��
��2�������ڴų���������Բ���˶������������˶��Ĺ켣���ҳ������˶��İ뾶��������������ṩ����������������Ÿ�Ӧǿ�ȣ�
��3�������˶������ڵ������ӷֱ��ڵ糡����ų����˶�ʱ��ĺͣ�����˶��Ĺ켣���ֱ��������ʱ�伴�ɣ�
��� �⣺��1�������ڵ糡���ؼ���ķ���������ֱ���˶�����������a��b����˶�ʱ��Ϊt1��t1=$\frac{L}{v}$��
�ص糡�ߵķ���$\frac{1}{2}L=\frac{0+{v}_{y}}{2}•{t}_{1}$
���ԣ�vy=v
֪����ǡ�ô�a��b���Ҳ��Ե�����Ӵ����ɳ�ʱ�ٶȴ�СΪ��$v��=\sqrt{{v}^{2}+{v}_{y}^{2}}=\sqrt{2}v$
�����ڵ糡���˶����糡���������ã�qE$\frac{1}{2}$L=$\frac{1}{2}$m��$\sqrt{2}$v��2-$\frac{1}{2}$mv2
�����ã�E=$\frac{m{v}^{2}}{qL}$
��2�������֪�����ӻص�O�����ٶ�Ϊv���ڼ������������Բ���˶�����ͼ��֪�����Ӵ�O��ص�O������Բ���˶��뾶R=L������Ϊv����
qvB=$\frac{m{v}^{2}}{L}$
�ã�B=$\frac{mv}{qL}$
��3�����������˶��Ĺ켣��ͼ��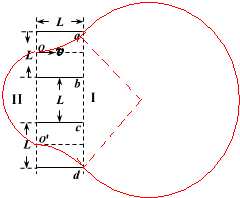
�������ڰ��Ҳ�������˶�ʱ��Ϊt2����c��d����˶�ʱ��Ϊt3���ڰ����������˶�ʱ��Ϊt4�����˶��Գ���֪t3=t1
���Ӵ�O��O'�ص�O���������˶�������T=2t1+t2+t4
��������糡ʱ�ٶȵķ�����ˮƽ����֮��ļнǣ�$tan��=\frac{{v}_{y}}{v}=\frac{v}{v}=1$
���ԣ���=45��������ͼ�м��ι�ϵ��֪�������ڼ����Ҳ��˶��İ뾶��${r}_{1}=\frac{\frac{3}{2}L}{cos45��}$=$\frac{{3\sqrt{2}L}}{2}$
�����˶����ǣ�t2=$\frac{\frac{3}{4}��2��{r}_{1}}{\sqrt{2}v}=\frac{9��L}{4v}$
�����ڼ���������˶��켣�ǰ��Բ�ܣ����ԣ�t4=$\frac{1}{2}•\frac{2��{r}_{2}}{v}=\frac{��L}{v}$
���Ӵ�O��O'�ص�O���������˶�������T=��2+$\frac{13��}{4}$��$\frac{L}{v}$
�𣺣�1����ǿ�糡�糡ǿ�ȴ�С��$\frac{m{v}^{2}}{qL}$��
��2������II�Ĵų���Ӧǿ�ȴ�С��$\frac{mv}{qL}$��
��3�����Ӵ�O��O��ص�O���������˶��������ǣ�2+$\frac{13��}{4}$��$\frac{L}{v}$��
���� ���⿼�������ڵ糡����ų��е��˶������չ淶���IJ��裬���������˶��Ĺ켣����ϼ��ι�ϵ���ҳ����еij��ȹ�ϵ��Ƕȹ�ϵ��������ȷ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��A��B�������A���ƹ�С����P��ϸ�����ң�B���ڴֲڵ�ˮƽ�����ϣ�����P��һ��б����ϵ���컨���ϵ�O�㣬O��������ϸ�ߵĽ�㣬ϸ��bO��ˮƽ��������B��cO������ֱ�������ŵ��ɣ����ɡ�ϸ�ߡ�С���ֵ��������ƣ�ϸ���뻬��֮���Ħ�����ɺ��ԣ�����װ�ô��ھ�ֹ״̬��������С���ֵ�б���е�������F=20$\sqrt{3}$ N����cO��a=120�㣬�������ٶ�gȡ10m/s2��������˵����ȷ���ǣ�������
��ͼ��ʾ��A��B�������A���ƹ�С����P��ϸ�����ң�B���ڴֲڵ�ˮƽ�����ϣ�����P��һ��б����ϵ���컨���ϵ�O�㣬O��������ϸ�ߵĽ�㣬ϸ��bO��ˮƽ��������B��cO������ֱ�������ŵ��ɣ����ɡ�ϸ�ߡ�С���ֵ��������ƣ�ϸ���뻬��֮���Ħ�����ɺ��ԣ�����װ�ô��ھ�ֹ״̬��������С���ֵ�б���е�������F=20$\sqrt{3}$ N����cO��a=120�㣬�������ٶ�gȡ10m/s2��������˵����ȷ���ǣ�������| A�� | ���ɵĵ���Ϊ20N | B�� | ����A������Ϊ2$\sqrt{3}$kg | ||
| C�� | ���������B��Ħ����Ϊ10$\sqrt{3}$N | D�� | ϸ��OP����ֱ����ļн�Ϊ60�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����Ƶ�����10N��OA���붥���ļн�Ϊ45��OB��ˮƽ����
��ͼ��ʾ����Ƶ�����10N��OA���붥���ļн�Ϊ45��OB��ˮƽ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾΪ���ֱ�ѵ����һ����Ŀ����ˮ�渡̨��б��֮������һ���������Ҳ����쳤�����������ӵ�����ΪO��������ֱƽ���ڰڶ���ʿ����б�����¹�����ץס�������°ڶ������ڶ�����͵�ʱ��ʿ���ɿ����ӣ�Ȼ����ƽ���˶��䵽ˮ�渡̨�ϣ��ɽ�ʿ����Ϊ�ʵ㣮��֪������l=5m��O���븡̨����A��ˮƽ����s=10m��O���븡̨�����ֱ�߶�h=10m��ʿ������Ϊm=60kg��g=10m/s2����
��ͼ��ʾΪ���ֱ�ѵ����һ����Ŀ����ˮ�渡̨��б��֮������һ���������Ҳ����쳤�����������ӵ�����ΪO��������ֱƽ���ڰڶ���ʿ����б�����¹�����ץס�������°ڶ������ڶ�����͵�ʱ��ʿ���ɿ����ӣ�Ȼ����ƽ���˶��䵽ˮ�渡̨�ϣ��ɽ�ʿ����Ϊ�ʵ㣮��֪������l=5m��O���븡̨����A��ˮƽ����s=10m��O���븡̨�����ֱ�߶�h=10m��ʿ������Ϊm=60kg��g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ����DIS�����������ij��ѧʵ���й����ϵĹ�ǿ�ֲ�ͼ��
��ͼ����DIS�����������ij��ѧʵ���й����ϵĹ�ǿ�ֲ�ͼ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ij̽��ѧϰС���ͬѧ����֤�����ܶ�������������ʵ������װ��һ����ͼ��ʾ��װ�ã��������ǻ��ҵ��˴���ʱ�����õ�ѧ����Դ�����ߡ���дֽ��ֽ����Сľ�顢ϸɳ���̶ȳߣ�������������ֽ������ϸ��ͨ�����ֹ��Ͽյ�СɳͰʱ���ͷ�СͰ�����鴦�ھ�ֹ״̬��������С���е�һλ��Ա��Ҫ��ɸ���ʵ�飬��
ij̽��ѧϰС���ͬѧ����֤�����ܶ�������������ʵ������װ��һ����ͼ��ʾ��װ�ã��������ǻ��ҵ��˴���ʱ�����õ�ѧ����Դ�����ߡ���дֽ��ֽ����Сľ�顢ϸɳ���̶ȳߣ�������������ֽ������ϸ��ͨ�����ֹ��Ͽյ�СɳͰʱ���ͷ�СͰ�����鴦�ھ�ֹ״̬��������С���е�һλ��Ա��Ҫ��ɸ���ʵ�飬���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������



�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��Ϊv=$\sqrt{gR}$�����Ի����ٶ���R��������� | |
| B�� | ��Ϊv=$\sqrt{\frac{GM}{R}}$�����Ի����ٶ���R�������С | |
| C�� | ��ΪF=$\frac{GMm}{R2}$�����Ե�R����ԭ����2��ʱ�������������������Ϊԭ����$\frac{1}{4}$ | |
| D�� | ��ΪF=$\frac{m{v}^{2}}{R}$�����Ե�R����ԭ����2��ʱ�������������������Ϊԭ����$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���о���Ÿ�Ӧ����ʵ����������ģ���ʵ�߽�������о����ȦA����Դ�������������Ϳ������ӳ�ԭ��Ȧ��·����С���̵���������ȦB���ӳɸ���Ȧ��·�����оٳ���ʵ���иı丱��Ȧ��·��ͨ����ʹ����Ȧ��·������Ӧ���������ַ�ʽ��
��ͼ��ʾ���о���Ÿ�Ӧ����ʵ����������ģ���ʵ�߽�������о����ȦA����Դ�������������Ϳ������ӳ�ԭ��Ȧ��·����С���̵���������ȦB���ӳɸ���Ȧ��·�����оٳ���ʵ���иı丱��Ȧ��·��ͨ����ʹ����Ȧ��·������Ӧ���������ַ�ʽ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com