
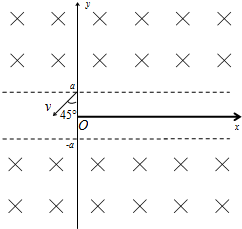
 在如图所示的xoy平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场.一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.已知粒子质量为m,电荷量为q,磁感应强度的大小B=$\frac{\sqrt{2}mv}{4qa}$.不计粒子的重力.
在如图所示的xoy平面直角坐标系中,一足够长绝缘薄板正好和x轴的正半轴重合,在y>a和y<-a的区域内均分布着方向垂直纸面向里的相同的匀强磁场.一带正电粒子,从y轴上的(0,a)点以速度v沿与y轴负向成45°角出射.带电粒子与挡板碰撞前后,x方向的分速度不变,y方向的分速度反向、大小不变.已知粒子质量为m,电荷量为q,磁感应强度的大小B=$\frac{\sqrt{2}mv}{4qa}$.不计粒子的重力.分析 (1)作出粒子的运动轨迹,根据半径公式求出粒子在磁场中运动的半径,结合几何关系求出粒子进入下方磁场后第一次打在绝缘板上的位置.
(2)根据几何关系求出板上开这一小孔可能的位置坐标.
(3)根据转过的弧长和速度求出运动的时间,注意圆周运动的周期性.
解答 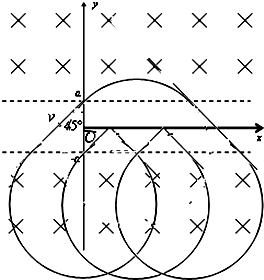 解:(1)粒子的轨迹如图所示,已知$B=\frac{{\sqrt{2}mv}}{4qa}$
解:(1)粒子的轨迹如图所示,已知$B=\frac{{\sqrt{2}mv}}{4qa}$
由 $qvB=m\frac{v^2}{r}$,
得 $r=2\sqrt{2}a$
下磁场区域中弦长 l=2rsin45°=4a
所以第一次击中点的坐标x=4a-2a-a=a
(2)开孔位置x=6na+a
或 x=6na+5a(n=0,1,2,3,…)
(3)若开孔位置在x=a,所用时间为${t_1}=\frac{{2\sqrt{2}a}}{v}+\frac{{2\sqrt{2}a+\frac{3}{2}πr}}{v}=\frac{{4\sqrt{2}a+3\sqrt{2}πa}}{v}$.
所以在x=6na+a处开孔,粒子运动的时间表达式为${t_{n1}}=\frac{{4\sqrt{2}a+3\sqrt{2}πa}}{v}+n(\frac{{2\sqrt{2}a}}{v}+3×\frac{{2\sqrt{2}a+\frac{3}{2}πr}}{v}+\frac{{\frac{1}{2}πr}}{v})=\frac{{(4+3π)\sqrt{2}a}}{v}+n×\frac{{(4+5π)2\sqrt{2}a}}{v}$(n=0,1,2,…)
若开孔在位置x=5a,所用时间为${t_2}=\frac{{2\sqrt{2}a}}{v}+3×\frac{{2\sqrt{2}a+\frac{3}{2}πr}}{v}+1×\frac{{\frac{π}{2}r}}{v}=\frac{{(4+5π)2\sqrt{2}a}}{v}$
所以在x=6na+5a处开孔,粒子运动的时间表达式为${t_{n2}}=(n+1)t_2^{\;}=(n+1)\frac{{(4+5π)2\sqrt{2}a}}{v}$(n=0,1,2,…)
(或写成 ${t_{n2}}=nt_2^{\;}=n\frac{{(4+5π)2\sqrt{2}a}}{v}$(n=1,2,3,…)
答:(1)粒子进入下方磁场后第一次打在绝缘板上的位置坐标为a.
(2)板上开这一小孔可能的位置坐标为x=6na+a或 x=6na+5a(n=0,1,2,3,…)
(3)在x=6na+a处开孔,运动的时间为$\frac{(4+3π)\sqrt{2}a}{v}+n×\frac{(4+5π)2\sqrt{2}a}{v}$,在x=6na+5a处开孔,粒子运动的时间为$n\frac{(4+5π)2\sqrt{2}a}{v}$(n=1,2,3,…)
点评 本题考查了带电粒子在磁场中的运动,难度较大,对数学能力的要求较高,关键作出轨迹图,结合半径公式、周期公式进行求解,根据周期性得出通项表达式是关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中物理 来源: 题型:解答题
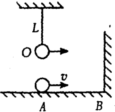 如图所示,单摆的摆长为L,当单摆摆球经过平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球,同时经过O正下方A点在光滑水平面上向右运动,与竖直墙壁碰撞后以原速度返回,求B、A间距x满足什么条件,才能使小球返回A点时,摆球恰好经过平衡位置O?(球与墙碰撞时间不计)
如图所示,单摆的摆长为L,当单摆摆球经过平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球,同时经过O正下方A点在光滑水平面上向右运动,与竖直墙壁碰撞后以原速度返回,求B、A间距x满足什么条件,才能使小球返回A点时,摆球恰好经过平衡位置O?(球与墙碰撞时间不计)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )
一个匝数为N=100的线圈在匀强磁场中匀速转动,产生的感应电动势的图象如图所示,下列说法正确的是( )| A. | 0.15s时刻,线圈处于与中性面相互垂直的位置 | |
| B. | 0.01s时刻,穿过线圈的磁通量为0 | |
| C. | 线圈转动的角速度为50πrad/s | |
| D. | 穿过线圈的磁通量变化率的最大值为22Wb/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
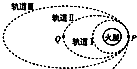 面向全球招募志愿者移民火星的“火星一号”计划,2015年2月22日公布了男女各100人的候选名单,4名华人入围.这个计划的疯狂之处在于这是一个有去无回的旅行.假设将来技术成熟,一艘飞船从火星返回地球时,经历了如图所示的变轨过程,则下列说法中正确的是( )
面向全球招募志愿者移民火星的“火星一号”计划,2015年2月22日公布了男女各100人的候选名单,4名华人入围.这个计划的疯狂之处在于这是一个有去无回的旅行.假设将来技术成熟,一艘飞船从火星返回地球时,经历了如图所示的变轨过程,则下列说法中正确的是( )| A. | 飞船在轨道Ⅱ上运动时,在P点的速度大于在Q点的速度 | |
| B. | 飞船在轨道Ⅰ上运动时的机械能大于轨道Ⅱ上运动时的机械能 | |
| C. | 飞船在轨道Ⅰ上运动到P点时的加速度小于飞船在轨道Ⅱ上运动到P点时的加速度 | |
| D. | 飞船绕火星在轨道Ⅰ上运动周期跟飞船返回地面的过程中绕地球以同样半径做圆周运动的周期相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
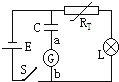 如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )
如图所示.E为电源,其内电阻不可忽略,RT为热敏电阻,其阻值随温度升高而减小,L为指示灯泡,C为平行板电容器,G为灵敏电流计.闭合开关S,当环境的温度明显升高时,下列说法正确的是( )| A. | 灯泡L变亮 | B. | 热敏电阻RT两端电压变大 | ||
| C. | 电容器C所带电荷量保持不变 | D. | 电流计G中电流方向由a到b |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
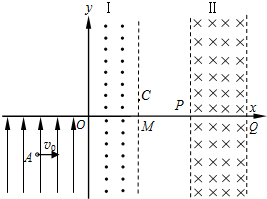 如图所示,在直角坐标系xoy的第一、四象限内存在边界平行y轴的两个有界匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ.O、M、P、Q为磁场边界和x轴的交点,OM=MP=L;在第三象限内存在沿y轴正方向的匀强电场.一质量为m,带电量为+q的带电粒子从电场中坐标为(-$\frac{2\sqrt{3}L}{3}$,-L)的A点以速度v0沿+x方向射出,恰好经过原点O射入区域Ⅰ,从C点射出区域Ⅰ,从某点射入区域Ⅱ,射入时速度与+x轴方向成30°角斜向下.经区域Ⅱ的磁场偏转后又从C点进入区域Ⅰ.求:
如图所示,在直角坐标系xoy的第一、四象限内存在边界平行y轴的两个有界匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ.O、M、P、Q为磁场边界和x轴的交点,OM=MP=L;在第三象限内存在沿y轴正方向的匀强电场.一质量为m,带电量为+q的带电粒子从电场中坐标为(-$\frac{2\sqrt{3}L}{3}$,-L)的A点以速度v0沿+x方向射出,恰好经过原点O射入区域Ⅰ,从C点射出区域Ⅰ,从某点射入区域Ⅱ,射入时速度与+x轴方向成30°角斜向下.经区域Ⅱ的磁场偏转后又从C点进入区域Ⅰ.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
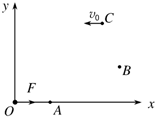 如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:
如图所示,在光滑水平面内建立直角坐标系xOy,一质点在该平面内O点受大小为F的力作用从静止开始做匀加速直线运动,经过t时间质点运动到A点,A、O两点距离为a,在A点作用力突然变为沿y轴正方向,大小仍为F,再经t时间质点运动到B点,在B点作用力又变为大小等于4F、方向始终与速度方向垂直且在该平面内的变力,再经一段时间后质点运动到C点,此时速度方向沿x轴负方向.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 扩散现象说明物质的分子在做永不停息的无规则运动 | |
| B. | 压缩气体时气体会表现出抗拒压缩的力是由于气体分子间存在斥力的缘故 | |
| C. | 两个分子距离减小时,分子间引力和斥力都在增大 | |
| D. | 两个分子间的距离为r0时,分子势能为0 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,在“研究平抛物体的运动”的实验中,用一张印有小方格的纸记录轨迹,小方格的边长为L=1.25cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度v0=0.7m/s (g取9.8m/s2),小球从a运动到d的时间0.1s,d点竖直方向的速率是1m/s.(保留一位有效数字)
如图所示,在“研究平抛物体的运动”的实验中,用一张印有小方格的纸记录轨迹,小方格的边长为L=1.25cm,若小球在平抛运动途中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度v0=0.7m/s (g取9.8m/s2),小球从a运动到d的时间0.1s,d点竖直方向的速率是1m/s.(保留一位有效数字)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com