
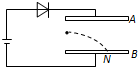
 ��ͼ��ʾ��ƽ�а������AB������ˮƽ���ã�A���Ϸ���B���·����ֽ���Ͷ����ܴ������ڵ�Դ�ϣ���֪A�͵�Դ���������������ܾ��е����ԣ�һ����С����AB ����ˮƽ���룬����B�����ϵ�N�㣬С����������ܺ��ԣ���ͨ�������ƶ�A�����ı�������AB��ࣨ��������ƽ�У���������˵����ȷ���ǣ�������
��ͼ��ʾ��ƽ�а������AB������ˮƽ���ã�A���Ϸ���B���·����ֽ���Ͷ����ܴ������ڵ�Դ�ϣ���֪A�͵�Դ���������������ܾ��е����ԣ�һ����С����AB ����ˮƽ���룬����B�����ϵ�N�㣬С����������ܺ��ԣ���ͨ�������ƶ�A�����ı�������AB��ࣨ��������ƽ�У���������˵����ȷ���ǣ�������| A�� | ��С������磬��A B�������ʱ��С�������N�� | |
| B�� | ��С������磬��A B����Сʱ��С�����N����� | |
| C�� | ��С������磬��A B�������ʱ��С�����N���ҵ� | |
| D�� | ��С������磬��A B����Сʱ��С����ܴ���N����� |
���� A��������磬B��������磬���ݶ����ܾ��е����ԣ�����ĵ���ֻ�����Ӳ��ܼ�С�������������糡�ı仯���жϵ糡���ı仯���Ӷ�ȷ��С��ˮƽ�����ϵ�λ�Ʊ仯��
��� �⣺A����С������磬��d����ʱ�����ݼ�С����Q�����ܼ�С������Q���䣬����E=$\frac{U}{d}$=$\frac{Q}{Cd}$=$\frac{4��kQ}{?S}$��֪E�������Ե糡�����䣬С����Ȼ����N�㣮��A��ȷ��
B����С������磬��d��Сʱ����������Q������E=$\frac{U}{d}$��֪d��СʱE�������Ե糡����������£�С����ƽ���˶���ֱ������ٶ������˶�ʱ���̣�����N����࣮��B��ȷ��
C����С������磬��AB���d����ʱ�����ݼ�С����Q�����ܼ�С������Q���䣬����E=$\frac{U}{d}$=$\frac{Q}{Cd}=\frac{4��kQ}{?S}$��֪E���䣬���Ե糡����С���䣬�����Ϊ���ϣ����糡��С��������С������ƽ���˶���ֱ�����ϵļ��ٶȲ��䣬�˶�ʱ�䲻�䣬С����Ȼ���ܴ���N�㣮��C����
D����С������磬��AB���d��Сʱ������������Q������E=$\frac{U}{d}$��֪E�������Ե糡����������ϣ����糡��С��������С������ƽ���˶���ֱ�����ϵļ��ٶȼ�С���˶�ʱ��䳤��С����N����Ҳ࣮��D����
��ѡ��AB��
���� �������Ĺؼ����մ�����ƽ���˶��ķ������Լ�֪�������ܵĵ����ԣ��ڱ����е������Ĵ�����ֻ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{4}$c | B�� | $\frac{1}{4}$c | C�� | $\frac{3}{4}$c | D�� | c |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
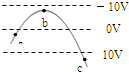 ��ͼ��ʾ������ƽ�еȾ�����߱�ʾ�糡�е����������棬����ֵ�ֱ�Ϊ-10V��0V��10V��ʵ����һ�������ӣ�ֻ�ܵ糡�����ڸ������ڵ��˶��켣��a��b��cΪ�켣�����㣮����˵����ȷ���ǣ�������
��ͼ��ʾ������ƽ�еȾ�����߱�ʾ�糡�е����������棬����ֵ�ֱ�Ϊ-10V��0V��10V��ʵ����һ�������ӣ�ֻ�ܵ糡�����ڸ������ڵ��˶��켣��a��b��cΪ�켣�����㣮����˵����ȷ���ǣ�������| A�� | ���ӿ��ܴ����磬Ҳ���ܴ����� | |
| B�� | �������������ܵĵ糡��Fa=Fb=Fc | |
| C�� | �������ȱ����˶� | |
| D�� | ����������ĵ����ܴ�СΪEpc��Epa��Epb |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
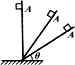 ��ͼ��ʾ����С��������Ϊ�ȵĹ⻬б���ϵ�A���ɾ�ֹ���£�Ȼ����������Ƚǵ������½��ж��ʵ�飬����˵����ȷ���ǣ�������
��ͼ��ʾ����С��������Ϊ�ȵĹ⻬б���ϵ�A���ɾ�ֹ���£�Ȼ����������Ƚǵ������½��ж��ʵ�飬����˵����ȷ���ǣ�������| A�� | ����ʱ�������� | B�� | ����ļ��ٶ���С | ||
| C�� | ����˵Ķ��ܲ��� | D�� | ����������ƽ������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
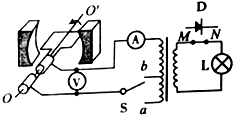 ��ͼ��ʾ��һ����ΪN=100�ľ�����Ȧ�����S=0.01m2�����費�ƣ��ƴ�ֱ�ڴŸ��ߵĶԳ���OO������ת��������Ȧ�����Ĵų�Ϊ��ǿ�ų����Ÿ�Ӧǿ��B=2T����Ȧͨ��-�����ѹ����һ���С�6V��3W�������ĵ���L����ѹ��ԭ��Ȧ��������Ϊn1=200�ѣ�b��ԭ��Ȧ�����ij�ͷ������Ȧ������Ϊn2=20�ѣ�������S����bλ��ʱ��С����ǡ���������⣬��С���ݵĵ��費���¶ȷ����仯��������
��ͼ��ʾ��һ����ΪN=100�ľ�����Ȧ�����S=0.01m2�����費�ƣ��ƴ�ֱ�ڴŸ��ߵĶԳ���OO������ת��������Ȧ�����Ĵų�Ϊ��ǿ�ų����Ÿ�Ӧǿ��B=2T����Ȧͨ��-�����ѹ����һ���С�6V��3W�������ĵ���L����ѹ��ԭ��Ȧ��������Ϊn1=200�ѣ�b��ԭ��Ȧ�����ij�ͷ������Ȧ������Ϊn2=20�ѣ�������S����bλ��ʱ��С����ǡ���������⣬��С���ݵĵ��費���¶ȷ����仯��������| A�� | ��·�е�ѹ���Ķ���Ϊ30$\sqrt{2}$V | |
| B�� | ��·�е������Ķ���$\frac{\sqrt{2}}{10}$A | |
| C�� | ��Ȧת���Ľ��ٶ�15$\sqrt{2}$rad/s | |
| D�� | ��������S����aλ�ã�����һ�����������D�ӵ�MN֮�䣬�����������䣬���ʱ��Ȧ�ṩ�Ĺ���Ϊ$\frac{3}{4}$W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
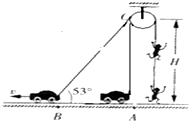 ��������ij��¥���������Ƭ��Ҫ���ؼ���Ա�ӵ���ɵ��ݶ�����ͼ��ʾ���ؼ���Ա����m=50kg�����������H=12m�������˶����֣��������ͼ��Aλ����v=10m/s����ǰ����Bλ��ʱ����BO��ˮƽ����ļн�Ϊ53�㣬��������Aλ���˶���Bλ�õĹ����У�gȡ10m/s2��sin53��=0.8��cos53��=0.6����������
��������ij��¥���������Ƭ��Ҫ���ؼ���Ա�ӵ���ɵ��ݶ�����ͼ��ʾ���ؼ���Ա����m=50kg�����������H=12m�������˶����֣��������ͼ��Aλ����v=10m/s����ǰ����Bλ��ʱ����BO��ˮƽ����ļн�Ϊ53�㣬��������Aλ���˶���Bλ�õĹ����У�gȡ10m/s2��sin53��=0.8��cos53��=0.6����������| A�� | ��Ա������ֱ���˶� | |
| B�� | ��Ա����ٶ�Ϊ8m/s | |
| C�� | �Ե���Ϊ�������ܵ���㣬��Ա����е��Ϊ2400J | |
| D�� | ��˿������һ�����ж���Ա����Ϊ900J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
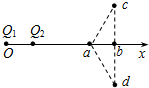 ��ͼ��ʾ�������������������������Q1��Q2�̶���x���ϣ�����Q1��Q2��������acdΪ���������Σ�cd����x�ᴹֱ����x���ཻ��b�㣬������˵����ȷ���ǣ�������
��ͼ��ʾ�������������������������Q1��Q2�̶���x���ϣ�����Q1��Q2��������acdΪ���������Σ�cd����x�ᴹֱ����x���ཻ��b�㣬������˵����ȷ���ǣ�������| A�� | a�㳡ǿС��b�㳡ǿ | |
| B�� | c����Ƶ���b����� | |
| C�� | c����Ƶ���d����� | |
| D�� | �����Ӵ�a���Ƶ�b�����Ƶ�c����������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼһ�������쳤��������ΪL��һ��������ס����һ��ϵһ����Ϊm��С��ʹ���յ�һ����ˮƽ���������뾶ΪR�����ٶ�Ϊ�ص�����Բ���˶�����ʹ��ʼ����뾶ΪR��Բ���У�С��Ҳ����ͬһˮƽ����������Բ���˶��������������Ĺ���ΪP������˵����ȷ���ǣ�������
��ͼһ�������쳤��������ΪL��һ��������ס����һ��ϵһ����Ϊm��С��ʹ���յ�һ����ˮƽ���������뾶ΪR�����ٶ�Ϊ�ص�����Բ���˶�����ʹ��ʼ����뾶ΪR��Բ���У�С��Ҳ����ͬһˮƽ����������Բ���˶��������������Ĺ���ΪP������˵����ȷ���ǣ�������| A�� | С��������Բ���˶������ٶȴ�СΪv=��$\sqrt{{R}^{2}+{L}^{2}}$ | |
| B�� | С�����˶��������ܵ���Ħ�����ķ���ָ��Բ�� | |
| C�� | С����ˮƽ��������������F=$\frac{P}{R��}$ | |
| D�� | С�����˶��������ܵ���Ħ�����Ĵ�Сf=$\frac{P}{��\sqrt{{R}^{2}+{L}^{2}}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com