
 如图所示,在水平面上有两条平行金属导轨MN、PQ,导轨间距为d,匀强磁场垂直于导轨所在的平面向里,磁感应强度大小为B,两根完全相同的金属杆1、2间隔一定的距离摆放在导轨上,且与导轨垂直,它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计,杆1以初速度v0滑向杆2,为使两杆不相碰,则杆2固定与不固定两种情况下,最初摆放两杆时的最少距离之比为( )
如图所示,在水平面上有两条平行金属导轨MN、PQ,导轨间距为d,匀强磁场垂直于导轨所在的平面向里,磁感应强度大小为B,两根完全相同的金属杆1、2间隔一定的距离摆放在导轨上,且与导轨垂直,它们的电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆的摩擦不计,杆1以初速度v0滑向杆2,为使两杆不相碰,则杆2固定与不固定两种情况下,最初摆放两杆时的最少距离之比为( )| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 1:1 |
分析 两个棒均不固定时,左边棒受向左的安培力,右边棒受向右的安培力,故左边棒减速,右边棒加速,两个棒系统动量守恒,根据动量守恒定律得到最后的共同速度,然后对右边棒运用动量定理列式;
当右边棒固定时,左边棒受向左的安培力,做减速运动,根据动量定理列式;
最后联立求解即可.
解答 解:金属杆1、2均不固定时,系统动量守恒,以向右问正方向,有:mv0=2mv,解得:v=$\frac{{v}_{0}}{2}$;
对右侧杆,采用微元法,以向右问正方向,根据动量定理,有:∑-F•△t=∑m△v,
其中:F=BIL=B•$\frac{BL({v}_{1}-{v}_{2})}{2R}$•L,
故:-∑$\frac{{{B^2}{L^2}({v_1}-{v_2})}}{2R}•△t$=∑m△v,
即$\frac{{B}^{2}{L}^{2}({l}_{2}-{l}_{1})}{2R}$=m•$\frac{{v}_{0}}{2}$,
解得:l1-l2=$\frac{{m{v_0}R}}{{{B^2}{L^2}}}$,即AB间的距离最小为x=$\frac{{m{v_0}R}}{{{B^2}{L^2}}}$;
当棒2固定后,对左侧棒,以向右问正方向,根据动量定理,有::∑-F•△t=∑m△v,
其中:F=BIL=B•$\frac{BLv}{2R}$•L,
故:-∑$\frac{{B}^{2}{L}^{2}v}{2R}•△t$=∑m△v,
即-$\frac{{{B^2}{L^2}l}}{2R}$=-mv0,
解得:l=$\frac{{2m{v_0}R}}{{{B^2}{L^2}}}$,故AB间的距离最小为x′=$\frac{{2m{v_0}R}}{{{B^2}{L^2}}}$;
故x′:x=2:1;
故ABD错误,C正确;
故选:C
点评 本题是力电综合问题,关键是明确两个导体棒均做变加速运动,要结合动量守恒定律和动量定理列式,同时要结合微元法思想分析,难度较大.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中物理 来源: 题型:选择题
| A. | 元电荷就是指电子本身 | |
| B. | 元电荷就是法拉第发现的 | |
| C. | 不论是摩擦起电还是感应起电,本质都是电荷的转移 | |
| D. | 摩擦起电是通过摩擦创造出了等量的异种电荷的过程 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 用长为L的金属导线将一小球A悬挂于O点,小球A在水平面内做匀速圆周运动,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,已知小球A做圆周运动的角速度为ω,金属导线与竖直方向的夹角为30°,求:金属导线中产生的感应电动势E.
用长为L的金属导线将一小球A悬挂于O点,小球A在水平面内做匀速圆周运动,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,已知小球A做圆周运动的角速度为ω,金属导线与竖直方向的夹角为30°,求:金属导线中产生的感应电动势E.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
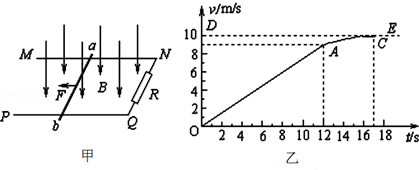
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
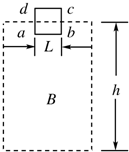 如图,正方形导线框abcd的边长为L=10cm,线框平面位于竖直平面内,上下两边处于水平状态.当它从某高处落下时通过一匀强磁场,磁场方向垂直于线框平面,线框的ab边刚进入磁场时,由于安培力的作用使得线框恰能匀速运动.已知磁场的宽度h=4L,线框刚进入磁场时的速度v0=2.5m/s.那么若以向下为力的正方向,则线框通过磁场区域过程中所受安培力的图象可能是以下四图中的( )
如图,正方形导线框abcd的边长为L=10cm,线框平面位于竖直平面内,上下两边处于水平状态.当它从某高处落下时通过一匀强磁场,磁场方向垂直于线框平面,线框的ab边刚进入磁场时,由于安培力的作用使得线框恰能匀速运动.已知磁场的宽度h=4L,线框刚进入磁场时的速度v0=2.5m/s.那么若以向下为力的正方向,则线框通过磁场区域过程中所受安培力的图象可能是以下四图中的( )| A. | 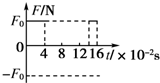 | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
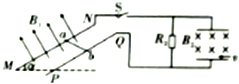 如图所示,两足够长的平行粗糙金属导轨MN,PQ相距L=1m.导轨平面与水平面夹角为α=30°.导轨电阻不计.磁感应强度B1=2T的匀强磁场垂直导轨平面向上,长L=1m的金属棒ab垂直于MN,PQ放置在导轨上,两者间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,金属棒的质量m1=2kg,电阻R1=lΩ,两金属棒导轨的上端连接右侧电路.电路和中通过导线接一对水平放置的平行金属板,两板间的距离和板长增为d=0.5m,定值电阻R2=3Ω,将金属棒由静止释放.重力加速度g取10m/s2,
如图所示,两足够长的平行粗糙金属导轨MN,PQ相距L=1m.导轨平面与水平面夹角为α=30°.导轨电阻不计.磁感应强度B1=2T的匀强磁场垂直导轨平面向上,长L=1m的金属棒ab垂直于MN,PQ放置在导轨上,两者间的动摩擦因数μ=$\frac{\sqrt{3}}{6}$,金属棒的质量m1=2kg,电阻R1=lΩ,两金属棒导轨的上端连接右侧电路.电路和中通过导线接一对水平放置的平行金属板,两板间的距离和板长增为d=0.5m,定值电阻R2=3Ω,将金属棒由静止释放.重力加速度g取10m/s2,查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 将两根粗糙的平行放置的直导轨MN、PQ固定在水平面上,左端与两根弯曲的光滑导轨平滑连接,在两水平导轨间存在两个磁场区,其中左侧的磁场方向竖直向上,磁感应强度大小为B,磁场的左边界位于水平导轨和弯曲导轨连接处;右侧的磁场方向竖直向下,磁感应强度大小为2B,如图所示,今将一导体棒b垂直导轨放置在右侧磁场的右边界处,导体棒a从弯曲导轨上距离水平面h高处由静止释放.已知两棒的质量均为m,二者在导轨间部分的电阻均为R,两导轨之间的距离为L,两导体棒与水平轨道间的动靡擦因数均为0.2,假设导体棒与导轨间的最大静摩擦力等于滑动摩擦力,整个运动过程中导体棒与导轨的接触始终良好,导轨的电阻不计,重力加速度为g.
将两根粗糙的平行放置的直导轨MN、PQ固定在水平面上,左端与两根弯曲的光滑导轨平滑连接,在两水平导轨间存在两个磁场区,其中左侧的磁场方向竖直向上,磁感应强度大小为B,磁场的左边界位于水平导轨和弯曲导轨连接处;右侧的磁场方向竖直向下,磁感应强度大小为2B,如图所示,今将一导体棒b垂直导轨放置在右侧磁场的右边界处,导体棒a从弯曲导轨上距离水平面h高处由静止释放.已知两棒的质量均为m,二者在导轨间部分的电阻均为R,两导轨之间的距离为L,两导体棒与水平轨道间的动靡擦因数均为0.2,假设导体棒与导轨间的最大静摩擦力等于滑动摩擦力,整个运动过程中导体棒与导轨的接触始终良好,导轨的电阻不计,重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,两条平行虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为l,金属圆环的直径也是l.圆环从左边界进入磁场,以垂直于磁场边界的恒定速度v穿过磁场区域.则下列说法正确的是( )
如图所示,两条平行虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为l,金属圆环的直径也是l.圆环从左边界进入磁场,以垂直于磁场边界的恒定速度v穿过磁场区域.则下列说法正确的是( )| A. | 感应电流的大小先增大后减小 | |
| B. | 感应电流的方向先逆时针后顺时针 | |
| C. | 金属圆环受到的安培力先向左后向右 | |
| D. | 进入磁场时感应电动势平均值$\overline{E}$=$\frac{1}{2}$πBav |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
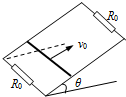 如图所示,倾角为θ=37°,间距L=0.30m且足够长的平行金属导轨电阻不计,处在磁感强度B=1.0T,方向垂直于导轨平面的匀强磁场中.导轨两端各接一个阻值R0=2.0Ω的电阻.在平行导轨间跨接一金属棒,金属棒质量m=1.0kg,电阻r=2.0Ω,与导轨间的动摩擦因数μ=0.50.金属棒以平行于导轨向上的初速度v0=10m/s上滑,已知它上升到最高点的过程中,通过上端电阻的电量q=0.10C,取g=10m/s2.求:
如图所示,倾角为θ=37°,间距L=0.30m且足够长的平行金属导轨电阻不计,处在磁感强度B=1.0T,方向垂直于导轨平面的匀强磁场中.导轨两端各接一个阻值R0=2.0Ω的电阻.在平行导轨间跨接一金属棒,金属棒质量m=1.0kg,电阻r=2.0Ω,与导轨间的动摩擦因数μ=0.50.金属棒以平行于导轨向上的初速度v0=10m/s上滑,已知它上升到最高点的过程中,通过上端电阻的电量q=0.10C,取g=10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com