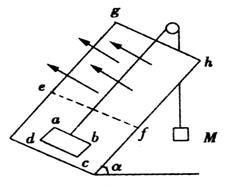
如图，光滑斜面的倾角
= 30°，在斜面上放置一矩形线框abcd，ab边的边长l1 = l m，bc边的边长l2= 0.6 m，线框的质量m = 1 kg，电阻R = 0.1Ω，线框通过细线与重物相连，重物质量M = 2 kg，斜面上ef线（ef∥gh）的右方有垂直斜面向上的匀强磁场，磁感应强度B = 0.5 T，如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef线和gh的距离s = 11.4 m，（取g = 10.4m/s2），求：
⑴线框进入磁场前重物M的加速度；
⑵线框进入磁场时匀速运动的速度v；
⑶ab边由静止开始到运动到gh线处所用的时间t；
⑷ab边运动到gh线处的速度大小和在线框由静止开始到运动到gh线的整个过程中产生的焦耳热．
【解析】（1）线框进入磁场前，线框仅受到细线的拉力FT，斜面的支持力和线框重力，重物M受到重力和拉力FT．对线框，由牛顿第二定律得FT – mg sinα= ma （2分）
联立解得线框进入磁场前重物M的加速度
= 5m/s2 （2分）
（2）因为线框进入磁场的最初一段时间做匀速运动，所以重物受力平衡Mg = FT′，
线框abcd受力平衡FT′= mg sinα + FA（1分）
ab边进入磁场切割磁感线，产生的电动势E = Bl1v 形成的感应电流
（1分）
受到的安培力
（1分）
联立上述各式得，Mg = mg sinα+
（1分）
代入数据解得v=6 m/s（1分）
（3）线框abcd进入磁场前时，做匀加速直线运动；进磁场的过程中，做匀速直线运动；进入磁场后到运动到gh线，仍做匀加速直线运动．
进磁场前线框的加速度大小与重物的加速度相同，为a = 5 m/s2
该阶段运动时间为
（1分）
进磁场过程中匀速运动时间
（1分）
线框完全进入磁场后线框受力情况同进入磁场前，所以该阶段的加速度仍为a = 5m/s2
解得：t3 =1.2 s（1分）
因此ab边由静止开始运动到gh线所用的时间为t = t1+t2+t3=2.5s （1分）
（4）线框ab边运动到gh处的速度v′=v + at3 = 6 m/s+5×1.2 m/s=12 m/s （1分）
整个运动过程产生的焦耳热Q = FAl2 =（Mg – mgsinθ）l2 = 9 J （3分）
阅读快车系列答案科目：高中物理 来源： 题型：
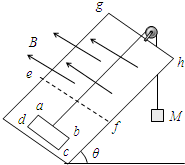（2011?顺义区一模）如图，光滑斜面的倾角为θ，斜面上放置一矩形导体线框abcd，ab边的边长为l1，bc边的边长为l2，线框的质量为m，电阻为R，线框通过细棉线绕过光滑的滑轮与重物相连，重物质量为M，斜面上ef线（ef平行底边）的右方有垂直斜面向上的匀强磁场，磁感应强度为B，如果线框从静止开始运动，在进入磁场的这段时间是做匀速运动的，且线框的ab边始终平行底边，则下列说法正确的是（ ）查看答案和解析>>
科目：高中物理 来源： 题型：
如图，光滑斜面的倾角α=30°，一个矩形导体线框abcd放在斜面内，ab边水平，长度l1=1m，bc边的长度l2=0.6m，线框的质量m=1kg，总电阻R=0.1Ω，线框通过细线与质量为m=2kg的重物相连，细线绕过定滑轮，不计定滑轮对细线的摩擦，斜面上水平线ef的右侧有垂直斜面向上的匀强磁场，磁感应强度B=0.5T，如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef线和斜面最高处gh（gh是水平的）的距离s=11.4m，取g=10m/s2，求：查看答案和解析>>
科目：高中物理 来源： 题型：
如图，光滑斜面的倾角α=30°，在斜面上放置一矩形线框abcd，ab边的边长l1=l m，bc边的边长l2=0.6m，线框的质量m=1kg，电阻R=0.1Ω，线框通过细线与重物相连，重物质量M=2kg，斜面上ef线（ef∥gh）的右方有垂直斜面向上的匀强磁场，磁感应强度B=0.5T，如果线框从静止开始运动，进入磁场最初一段时间是匀速的，ef线和gh的距离s=11.4m，（取g=10.4m/s2），求：查看答案和解析>>
科目：高中物理 来源： 题型：
如图，光滑斜面的倾角为θ，斜面上放置-矩形导体线框abcd，ab边的边长为l1，bc边的边长为l2，线框的质量为m、电阻为R，线框通过绝缘细线绕过光滑的小滑轮与重物相连，重物质量为M，斜面上ef线（ef平行底边）的右上方有垂直斜面向上的匀强磁场，磁感应强度为B，如果线框从静止开始运动，进入磁场的最初-段时间是做匀速运动的，且线框的ab边始终平行底边，则下列说法正确的是（ ）
如图，光滑斜面的倾角为θ，质量为m的物体在平行于斜面的轻质弹簧作用下处于静止状态，则（ ）