
 如图所示,质量m=0.10kg的靶盒B位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中的虚线区域.当靶盒B进入相互作用区域时便有向左的水平恒力F=50N作用.在P处有一固定的手枪A,它可根据需要瞄准靶盒每次发射一颗水平速度V0=100m/s、质量同样为m=0.10kg的子弹,当子弹打入靶盒B后,便留在盒内,碰撞时间极短.若每当靶盒B停在或到达O点时,就有一颗子弹进入靶盒B内,求:
如图所示,质量m=0.10kg的靶盒B位于光滑水平导轨上,开始时静止在O点,在O点右侧有范围很广的“相互作用区域”,如图中的虚线区域.当靶盒B进入相互作用区域时便有向左的水平恒力F=50N作用.在P处有一固定的手枪A,它可根据需要瞄准靶盒每次发射一颗水平速度V0=100m/s、质量同样为m=0.10kg的子弹,当子弹打入靶盒B后,便留在盒内,碰撞时间极短.若每当靶盒B停在或到达O点时,就有一颗子弹进入靶盒B内,求:分析 (1)第一颗子弹进入靶盒A后,根据碰撞过程系统动量守恒列出等式,再运用动能定理求解
(2)根据题意,A在的恒力F的作用返回O点时第二颗子弹正好打入,由于A的动量与第二颗子弹动量大小相同,方向相反,故第二颗子弹打入后,A将静止在O点.
由系统动量守恒和动能定理求解.
(3)运用归纳法得到第(2k-1)颗子弹打入后靶盒的运动速度,由能量守恒定律求出系统产生的热能表达式,再用同样的方法得到第2k颗子弹打入后系统产生的热能.
解答 解:(1)设第一课子弹进入靶盒B后,子弹与靶盒的共同速度为v1.取向右为正方向
由动量守恒定律有:mv0=(m+m)v1
设B离开O点的最大距离为s1,由动能定理得
-Fs1=0-$\frac{1}{2}(m+M){v}_{1}^{2}$
解得:s1=5m
(2)根据题意,B在恒力F的作用下返回O点时第二颗子弹正好打入,由于靶盒与第二颗子弹的动量之和为零,故第二颗子弹打入时,B将静止在O点.
第三颗子弹打入后,由系统动量守恒得
mv0=(3m+m)v3
B离开O点再回到O点,取碰后A运动的方向为正方向,由动量定理得
-Ft3=0-2(3m+m)v3
解得 t3=0.4s
(3)由第(2)问的计算可以看出,第(2k-1)颗子弹打入后,
靶盒的运动速度 mv0=[(2k-1)m+m)]v2k-1
系统产生的热能 Q2k-1=$\frac{1}{2}$mv02-$\frac{1}{2}$[(2k-1)m+m)]v2k-12=(1-$\frac{1}{2k}$)•$\frac{1}{2}m{v}_{0}^{2}$
第2k颗子弹打入后,靶盒静止不动,
系统动能全部转化为内能 Q2k=$\frac{1}{2}$mv02+$\frac{1}{2}$[(2k-1)m+m)]v2k-12=(1+$\frac{1}{2k}$)•$\frac{1}{2}m{v}_{0}^{2}$
当n为奇数时 Q总=Q1+Q2+…+Qn=$\frac{1}{2}m{v}_{0}^{2}$(n-$\frac{1}{n+1}$)=500(n-$\frac{1}{n+1}$)
当n为偶数时 Q总=Q1+Q2+…+Qn=$\frac{1}{2}m{v}_{0}^{2}$•n=500n
答:
(1)当第一颗子弹进入靶盒B后,靶盒B离开O点的最大距离是5m;
(2)求第三颗子弹进入靶盒B到第四颗子弹进入靶盒B的时间间隔是0.4s;
(3)弹与靶盒组成的系统所产生的内能为500(n-$\frac{1}{n+1}$)或500n.
点评 对于碰撞过程,其基本规律动量守恒定律要掌握牢固,并能正确运用.能把动量守恒定律和动能定理结合应用.


科目:高中物理 来源: 题型:计算题
 如图,质量M=1kg的长木板静止在光滑的水平面上,有一个质量m=0.2kg的可看作质点的物体以6m/s的水平初速度木板的左端冲上木板,在木板上滑行了2s后与木板保持相对静止,求:
如图,质量M=1kg的长木板静止在光滑的水平面上,有一个质量m=0.2kg的可看作质点的物体以6m/s的水平初速度木板的左端冲上木板,在木板上滑行了2s后与木板保持相对静止,求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题

| H(cm) | 4 | 8 | 10 | 12 | 14 | 20 |
| L(cm) | 50 | 50 | 50 | 60 | 70 | 100 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
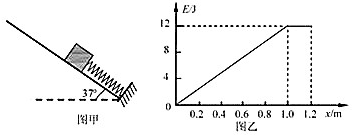
| A. | 在0-1.Om阶段,物体做均加速直线运动,其加速度大小为6m/s2 | |
| B. | 在1.0-1.2m阶段,物体做匀速直线运动,其速度大小为12m/s | |
| C. | 在上升过程中.物体的最大动能为6J | |
| D. | 若斜面足够长物体再次回到初始位置时其动能为18J |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | ${\;}_{6}^{14}C$经一次α衰变后成为${\;}_{7}^{14}C$ | |
| B. | ${\;}_{2}^{4}$He核由两个中子和两个质子组成 | |
| C. | 核反应方程应遵循质子数和中子数守恒 | |
| D. | 温度升高不能改变放射性元素的半衰期 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 已知地球半径R | |
| B. | 已知卫星绕地球做匀速圆周运动的轨道半径r和线速度v | |
| C. | 已知卫星绕地球做匀速圆周运动的线速度v和周期T | |
| D. | 已知地球公转的周期T′及运转半径r′ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

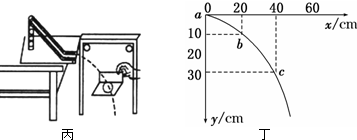
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
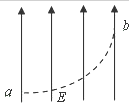 一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )
一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )| A. | 油滴带正电 | B. | 电势能增加 | ||
| C. | 动能增加 | D. | 重力势能和电势能之和增加 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com