
| A. | 密度之比 | B. | 第一宇宙速度之比 | ||
| C. | 表面重力加速度之比 | D. | 水星和金星绕太阳运动的周期之比 |
分析 根据密度公式$ρ=\frac{M}{V}$,即可判定密度之比;
根据第一宇宙速度表达式v=$\sqrt{\frac{GM}{R}}$,即可求得它们的第一宇宙速度之比;
依据重力等于引力,即可求解表面重力加速度之比;
根据引力提供向心力,结合轨道半径,即可求解周期之比.
解答 解:A、根据密度公式$ρ=\frac{M}{V}$,已知水星和金星两个星球的质量之比和半径之比,因此可求得它们的密度之比.故A正确.
B、根据第一宇宙速度表达式v=$\sqrt{\frac{GM}{R}}$,由于水星和金星的质量和体积之比可知,则可求出水星和金星的第一宇宙速度之比.故B正确.
C、根据g=$\frac{GM}{{R}^{2}}$ 知,知道质量与轨道半径各自之比,可以得出水星和金星的表面加速度之比,故C正确.
D、根据G$\frac{Mm}{{r}^{2}}$=mr$\frac{4{π}^{2}}{{T}^{2}}$ 得,r=$\sqrt{\frac{GM{T}^{2}}{4{π}^{2}}}$,根据水星和金星的轨道半径之比,才可以得出周期之比,由于轨道半径的不知,因此无法确定它们的周期之比,故D错误.
故选:ABC.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,本题注意天体的半径与天体的轨道半径不同是解题的关键.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
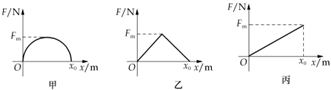
| A. | W1>W2>W3 | B. | W1>W2=W3 | ||
| C. | W1=W2=W3 | D. | 无法比较它们的大小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
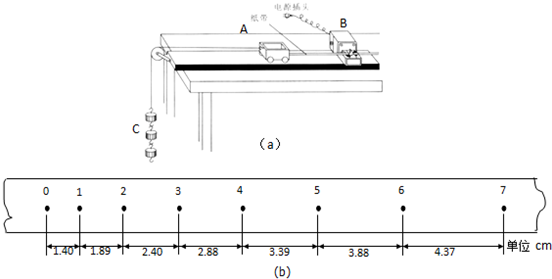
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
| 瞬时速度/(m/s) | 0.165 | 0.215 | 0.314 | 0.364 | 0.413 |
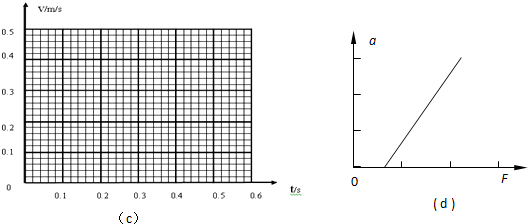
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球表面的重力加速度g月=$\frac{h{v}_{0}^{2}}{{L}^{2}}$ | |
| B. | 月球的平均密度ρ=$\frac{3h{v}_{0}^{2}}{2πG{L}^{2}R}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D. | 月球的质量m月=$\frac{h{R}^{2}{v}_{0}^{2}}{G{L}^{2}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
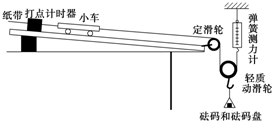

查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com