
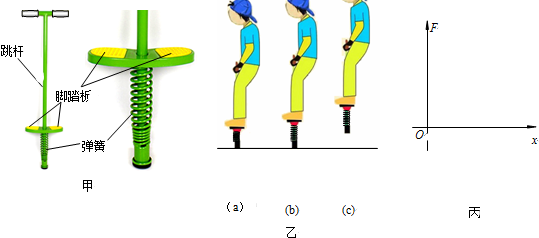
分析 (1)根据平衡条件以及胡克定律可求得劲度系数,并画出对应的图象;
(2)对全过程进行分析,根据机械能守恒定律可求得最大速度;
(3)分别对弹簧恢复原状和小孩抓住杆的过程由机械能守恒定律和动量守恒定律列式,联立即可求得最大高度.
解答 解:(1)小孩处于静止状态时,根据平衡条件有Mg=kx0
解得:k=$\frac{Mg}{{x}_{0}}$
F-x图如图所示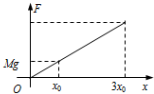
(2)利用F-x图象可知,图线与横轴所包围的面积大小等于弹簧弹力做功的大小.
弹簧压缩量为x时,弹性势能为Ep弾=$\frac{1}{2}$kx2
图a状态弹簧的弹性势能为Ep弾1=$\frac{1}{2}$k(3x0)2
小孩从图a至图b的过程,小孩先做加速运动后做减速运动,当弹簧弹力与重力等大时小孩向上运动的速度最大,设其最大速度为vmax
此时弹簧压缩量为x0,弹簧的弹性势能为Ep弾2=$\frac{1}{2}$kx2
从图a至小孩向上运动速度达到最大的过程中,小孩和弹簧系统机械能守恒,因此有:
$\frac{1}{2}$k(3x0)2=Mg(3x0-x0)+$\frac{1}{2}$Mv2+$\frac{1}{2}$kx2
解得:vmax=2$\sqrt{g{x}_{0}}$
(3)图a状态至弹簧长度为原长的过程中,小孩和弹簧系统机械能守恒.设小孩在弹簧长度为原长时的速度为v0,则有:
$\frac{1}{2}$k(3x0)2=Mg(3x0)+$\frac{1}{2}$Mv2
小孩迅速抓住跳杆的瞬间,内力远大于外力,小孩和弹跳杆系统动量守恒.
设小孩和弹跳杆共同速度为v1,规定竖直向上方向为正,有Mv0=(M+m)v1
小孩和弹跳杆一起竖直上升至最高点,小孩和弹跳杆系统机械能守恒,因此有:
$\frac{1}{2}$(M+m)v2=(M+m)ghmax
解得:hmax=$\frac{3{M}^{2}{x}_{0}}{2(M+m)^{2}}$
答:(1)弹跳杆中弹簧的劲度系数k为$\frac{Mg}{{x}_{0}}$,弹簧弹力F的大小随弹簧压缩量x变化的示意图如图所示;
(2)在图乙所示的过程中,小孩在上升阶段的最大速率为2$\sqrt{g{x}_{0}}$
(3)求在图乙所示的过程中,弹跳杆下端离地的最大高度为$\frac{3{M}^{2}{x}_{0}}{2(M+m)^{2}}$.
点评 本题考查机械能守恒定律的应用,要注意正确分析全过程,明确弹簧的弹性势能与重力势能之间的转化及守恒规律的应用;即注意能量转化的方向问题.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
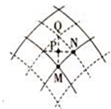 如图所示,某时刻两列频率相同、振幅为A的横波在叠加区域相遇,其中虚线表示波谷,实线表示波峰,相邻虚实线之间间隔距离为a,从虚线传播到相邻实线的时间为t,P点为QM的中点,其中M、N两点中振动始终加强的是M点,两列波的频率为$\frac{1}{2t}$,从图示时刻开始经2.5t的时间,P点的位移大小为2A.
如图所示,某时刻两列频率相同、振幅为A的横波在叠加区域相遇,其中虚线表示波谷,实线表示波峰,相邻虚实线之间间隔距离为a,从虚线传播到相邻实线的时间为t,P点为QM的中点,其中M、N两点中振动始终加强的是M点,两列波的频率为$\frac{1}{2t}$,从图示时刻开始经2.5t的时间,P点的位移大小为2A.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | X恒星质量与地球质量之比为$\frac{n{{T}_{2}}^{2}}{{{T}_{1}}^{2}}$ | |
| B. | X恒星质量与地球质量之比为$\frac{{n}^{3}{{T}_{2}}^{2}}{{{T}_{1}}^{2}}$ | |
| C. | 行星P运行速度与月球公转速度之比为$\frac{1}{\sqrt{n}}$ | |
| D. | 行星P运行速度与月球公转速度之比为$\frac{n{T}_{2}}{{T}_{1}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
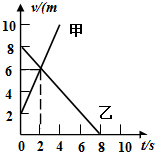
| A. | 甲沿正向做匀加速直线运动,乙沿反向做匀减速直线运动 | |
| B. | 甲比乙速度变化得快 | |
| C. | 2秒末甲乙相遇 | |
| D. | 2秒末甲乙速度相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
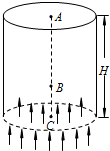 “娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比,人水平横躺时受风面积最大,设为S0,站立时受风面积为$\frac{1}{8}$S0;当受风面积为$\frac{1}{2}$S0时,表演者恰好可以静止或匀速漂移.如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.关于表演者下落的过程,下列说法中正确的是( )
“娱乐风洞”是一项将科技与惊险相结合的娱乐项目,它能在一个特定的空间内把表演者“吹”起来.假设风洞内向上的风量和风速保持不变,表演者调整身体的姿态,通过改变受风面积(表演者在垂直风力方向的投影面积),来改变所受向上风力的大小.已知人体所受风力大小与受风面积成正比,人水平横躺时受风面积最大,设为S0,站立时受风面积为$\frac{1}{8}$S0;当受风面积为$\frac{1}{2}$S0时,表演者恰好可以静止或匀速漂移.如图所示,某次表演中,人体可上下移动的空间总高度为H,表演者由静止以站立身姿从A位置下落,经过B位置时调整为水平横躺身姿(不计调整过程的时间和速度变化),运动到C位置速度恰好减为零.关于表演者下落的过程,下列说法中正确的是( )| A. | 从A至B过程表演者的加速度大于从B至C过程表演者的加速度 | |
| B. | 从A至B过程表演者的运动时间小于从B至C过程表演者的运动时间 | |
| C. | 从A至B过程表演者动能的变化量大于从B至C过程表演者克服风力所做的功 | |
| D. | 从A至B过程表演者动量变化量的数值小于从B至C过程表演者受风力冲量的数值 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
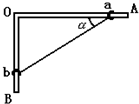 如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度$\frac{{v}_{a}}{{v}_{b}}$=( )
如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度$\frac{{v}_{a}}{{v}_{b}}$=( )| A. | tanα | B. | $\frac{1}{tanα}$ | C. | sinαcosα | D. | sin2α |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
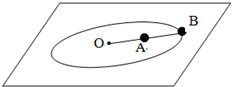 两根0.4m长的轻绳,其中OA的O端固定,另一端拴一质量m=0.4kg的A小球,另一根绳一端连在A上,另一端连着两一个同样的小球B.使其在光滑水平面上以ω=5rad/s的角速度做匀速圆周运动,求绳子OA的拉力为多大?若每根绳子能承受的最大拉力为27N,则绳断时,两小球的线速度分别为多大?
两根0.4m长的轻绳,其中OA的O端固定,另一端拴一质量m=0.4kg的A小球,另一根绳一端连在A上,另一端连着两一个同样的小球B.使其在光滑水平面上以ω=5rad/s的角速度做匀速圆周运动,求绳子OA的拉力为多大?若每根绳子能承受的最大拉力为27N,则绳断时,两小球的线速度分别为多大?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
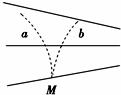 如图所示,实线为不知方向的三条电场线,从电场中M点垂直于电场线以相同速度飞出a、b两个带电粒子,运动轨迹如图中虚线所示,则( )
如图所示,实线为不知方向的三条电场线,从电场中M点垂直于电场线以相同速度飞出a、b两个带电粒子,运动轨迹如图中虚线所示,则( )| A. | 两个粒子的电势能一个增加一个减小 | |
| B. | 能判断a、b一定带异种电荷,但是不能判断电场的方向 | |
| C. | a的加速度将增加,b的加速度将增加 | |
| D. | 如果知道a带正电,该电场线一定是带正电的点电荷产生的电场 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com