
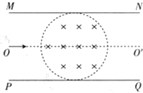
 如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求:
如图所示,平行板MN、PQ间距离为d,板长为2d,板的正中有一半径为$\frac{d}{2}$的圆形有界磁场,磁场边界刚好与两板相切,两板间所加电压为U,一质量为m,电量为q的带电粒子从左端沿两板间的中线向右射入两板间,若只撤去磁场,粒子刚好从上板右端N点射出,若只撤去两板间所加的电压,带电粒子恰好能从下板的右端Q点射出,不计粒子的重力,求:分析 (1)粒子在电场中做类平抛运动,在磁场中做匀速圆周运动,应用类平抛运动规律与牛顿第二定律可以求出磁感应强度.
(2)作出粒子运动轨迹,求出粒子轨道半径,应用牛顿第二定律求出临界速度,然后确定粒子速度范围.
解答 解:(1)撤去磁场,粒子在电场中做类平抛运动,
水平方向:2d=v0t,竖直方向:$\frac{1}{2}$d=$\frac{1}{2}$$\frac{qU}{md}$t2,解得:v0=2$\sqrt{\frac{qU}{m}}$,
撤去电场粒子在磁场中做匀速圆周运动,运动轨迹如图所示: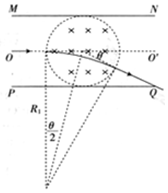
由几何知识得:tan$\frac{θ}{2}$=$\frac{\frac{d}{2}}{{R}_{1}}$=$\frac{sinθ}{1+cosθ}$,
sinθ=$\frac{\frac{d}{2}}{\sqrt{{d}^{2}+(\frac{d}{2})^{2}}}$,cosθ=$\frac{d}{\sqrt{{d}^{2}+(\frac{d}{2})^{2}}}$,解得:R1=(1+$\frac{\sqrt{5}}{2}$)d,
洛伦兹力提供向心力,由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{{R}_{1}}$,解得:B=$\frac{4(\sqrt{5}-2)}{d}$$\sqrt{\frac{mU}{q}}$;
(2)要使粒子刚好不从下板的左端射出粒子运动轨迹如图所示: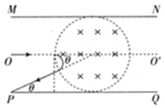
由几何知识得:tanθ=$\frac{\frac{d}{2}}{d}$=$\frac{1}{2}$,cosθ=$\frac{d}{\sqrt{{d}^{2}+(\frac{d}{2})^{2}}}$,
$\frac{d}{2}$=$\frac{d}{2}$tanθ+R2+$\frac{{R}_{2}}{cosθ}$,解得:R2=$\frac{(\sqrt{5}-2)d}{2}$,
洛伦兹力提供向心力,由牛顿第二定律得:
qv2B=m$\frac{{v}_{2}^{2}}{{R}_{2}}$,解得:v2=2($\sqrt{5}$-2)2$\sqrt{\frac{qU}{m}}$,
粒子速度大小范围:2($\sqrt{5}$-2)2$\sqrt{\frac{qU}{m}}$≤v≤2$\sqrt{\frac{qU}{m}}$;
答:(1)磁场的磁感应强度大小为$\frac{4(\sqrt{5}-2)}{d}$$\sqrt{\frac{mU}{q}}$;
(2)如果只撤去电场,要使粒子不能从板间射出,则粒子进入板间的速度大小应满足的条件是:2($\sqrt{5}$-2)2$\sqrt{\frac{qU}{m}}$≤v≤2$\sqrt{\frac{qU}{m}}$.
点评 本题考查了粒子在电场与磁场中的运动,分析清楚粒子运动过程、作出粒子运动轨迹、求出粒子轨道半径是解题的前提与关键,应用类平抛运动规律、牛顿第二定律可以解题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图坐标系xOy平面内,以x,y轴为界边长均为L的区域中,有场强大小均为E,方向如图的匀强电场,电场周围有垂直纸面向里的匀强磁场,在第Ⅰ象限内无限接近坐标原点O处有一电荷量为q、质量为m的带正电的粒子,由静止释放后依次分别经Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的电场区域和磁场区域,已知粒子在各个电场区域中均做直线运动,不考虑粒子重力.求:
如图坐标系xOy平面内,以x,y轴为界边长均为L的区域中,有场强大小均为E,方向如图的匀强电场,电场周围有垂直纸面向里的匀强磁场,在第Ⅰ象限内无限接近坐标原点O处有一电荷量为q、质量为m的带正电的粒子,由静止释放后依次分别经Ⅰ、Ⅱ、Ⅲ、Ⅳ象限的电场区域和磁场区域,已知粒子在各个电场区域中均做直线运动,不考虑粒子重力.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
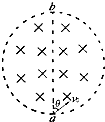 如图,半径为R的圆是与一圆柱形匀强磁场区域的横截面(纸面),ab为其直径,磁场的磁感应强度大小为B,方向垂直于纸面向里.一带电粒子以速率v0从a点沿与ab夹角θ=60°方向射入磁场,并从b点离开磁场.不计粒子重力.则粒子的比荷$\frac{q}{m}$为( )
如图,半径为R的圆是与一圆柱形匀强磁场区域的横截面(纸面),ab为其直径,磁场的磁感应强度大小为B,方向垂直于纸面向里.一带电粒子以速率v0从a点沿与ab夹角θ=60°方向射入磁场,并从b点离开磁场.不计粒子重力.则粒子的比荷$\frac{q}{m}$为( )| A. | $\frac{{v}_{0}}{BR}$ | B. | $\frac{{v}_{0}}{2BR}$ | C. | $\frac{\sqrt{3}{v}_{0}}{2BR}$ | D. | $\frac{\sqrt{3}{v}_{0}}{BR}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 某人站在力传感器上做“下蹲-起跳”的动作,力传感器显示此过程F-t图象如图所示,则下列判断正确的是( )
某人站在力传感器上做“下蹲-起跳”的动作,力传感器显示此过程F-t图象如图所示,则下列判断正确的是( )| A. | b点时人的速度为零 | B. | c点时人开始向上起跳 | ||
| C. | e点时加速度比b点大 | D. | a-c阶段处于下蹲过程中 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某同学在“研究平抛物体的运动”时,描绘平抛物体运动的轨迹,求物体平抛的初速度.如图所示,是用平滑的曲线画出平抛小球的运动轨迹.A、B、C是轨迹上的三点,以A点为坐标原点,B、C两点的坐标在图中标出,(取g=10m/s2)则
某同学在“研究平抛物体的运动”时,描绘平抛物体运动的轨迹,求物体平抛的初速度.如图所示,是用平滑的曲线画出平抛小球的运动轨迹.A、B、C是轨迹上的三点,以A点为坐标原点,B、C两点的坐标在图中标出,(取g=10m/s2)则查看答案和解析>>
科目:高中物理 来源: 题型:实验题
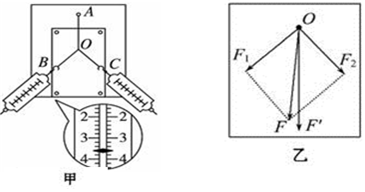
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
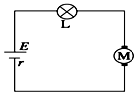 如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机正常工作,电动机的线圈电阻R=1.5Ω.求:
如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机正常工作,电动机的线圈电阻R=1.5Ω.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com