
 �й���������ѧ�ҡ��й���ѧԺԺʿ����۽�������1945���״�ͨ��ʵ��۲쵽���������ӵĵ�����ײ���̣������������õ糡���ų������������������������˶���������һ���̣�ʵ�����ԭ�����£�����ͼ��ʾ��xOyƽ���ڣ�A��C��С��ԭ��ľ����ΪL��ÿ��һ����ʱ��ԴԴ���ϵطֱ��A�����������ӣ�C�����븺���ӣ����ٶȾ�Ϊv0������ֱx�ᣬ���������ӵ�������Ϊm���������Ϊe�����Ե���֮�������ã�����y�����������һˮƽ���ҵ���ǿ�糡����y����Ҳ������һ��ֱֽ�����ǿ�ų���ͼ��δ��������Ҫʹ������������y���ϵ�P��0��L������������
�й���������ѧ�ҡ��й���ѧԺԺʿ����۽�������1945���״�ͨ��ʵ��۲쵽���������ӵĵ�����ײ���̣������������õ糡���ų������������������������˶���������һ���̣�ʵ�����ԭ�����£�����ͼ��ʾ��xOyƽ���ڣ�A��C��С��ԭ��ľ����ΪL��ÿ��һ����ʱ��ԴԴ���ϵطֱ��A�����������ӣ�C�����븺���ӣ����ٶȾ�Ϊv0������ֱx�ᣬ���������ӵ�������Ϊm���������Ϊe�����Ե���֮�������ã�����y�����������һˮƽ���ҵ���ǿ�糡����y����Ҳ������һ��ֱֽ�����ǿ�ų���ͼ��δ��������Ҫʹ������������y���ϵ�P��0��L���������������� ��1�������ӽ���糡������ƽ���˶�����ţ�ٵڶ����ɺ�λ��ʱ�乫ʽ��ϣ��������糡ǿ��E�Ĵ�С�������ӽ���ų���������Բ���˶��������֪�켣�뾶����L����ţ�ٵڶ����ɺ���������ʽ������B�Ĵ�С�������ֶ����ж�B�ķ���
��2���������ڵ糡���˶�ʱ���糡���������������ɶ��ܶ����������ǰ�����ӵĶ��ܣ�������ֱ����������ֱ���˶��Ĺ��ɣ�������˶�ʱ�䣬���������ڴų����˶�ʱ�������������������ܲ��䣬����ʱ��Ϊ$\frac{1}{4}$���ڣ��Ӷ������ʱ��
��3������������ȷû�������ĵ�ɵ��˶��켣���ɼ��ι�ϵ�����OD��ľ��룮
��� �⣺��1����C������ĸ����ӣ���ţ�ٵڶ����ɵã�
ev0B=$\frac{{mv}_{0}^{2}}{L}$
�ɵã�B=$\frac{m{v}_{0}}{eL}$
��������C�����ܵ������������������ֶ����жϿ�֪�ų�B�ķ���ֱֽ�����⣮
��2����A������������ӣ��ɶ��ܶ����ã�
EeL=EkA-$\frac{{mv}_{0}^{2}}{2}$
���� EkA=$\frac{5m{v}_{0}^{2}}{2}$
�� EkB=$\frac{1}{2}{mv}_{0}^{2}$
�� $\frac{{E}_{kA}}{{E}_{kB}}=\frac{5}{1}$
��C����ĸ������˶���ʱ��Ϊ��tB=$\frac{90��}{360��}��\frac{2��L}{{v}_{0}}$=$\frac{��L}{2{v}_{0}}$��
�������ڵ糡���˶���ʱ��Ϊ��tA=$\frac{L}{{v}_{0}}$
���t=tB-tA=$\frac{��L}{2{v}_{0}}$-$\frac{L}{{v}_{0}}$=$\frac{����-2��L}{2{v}_{0}}$
��3���������ڵ糡��ƫת��$tan��=\frac{v_y}{v_0}=\frac{at}{v_0}=2\frac{{\frac{1}{2}a{t^2}}}{{{v_o}t}}=2\frac{L}{L}=2$��
��$sin��=\frac{2}{{\sqrt{5}}}��cos��=\frac{1}{{\sqrt{5}}}$ ��P��û���븺���������������ӣ��ڵ�һ������ǿ�ų���˳ʱ����P���˶���D�㣮
��P��û���븺���������������ӣ��ڵ�һ������ǿ�ų���˳ʱ����P���˶���D�㣮
�������ڴų��еĹ���뾶Ϊ$r=\frac{{\sqrt{5}m{v_0}}}{qB}=\sqrt{5}R=\sqrt{5}L$����$O'P=O'D=\sqrt{5}L$
��ֱ��������PMO����$\begin{array}{l}PM=rsin��=2L\\ ��O'N=MO=PM-PO=L\\ MO'=rcos��=ON=L\end{array}$
��ֱ��������NDO���У��ɹ��ɶ�����O'D2=O'N2+ND2
��${��\sqrt{5}L��^2}={L^2}+N{D^2}$
��ND=2L
��OD=ON+ND=3L��
�𣺴Ÿ�Ӧǿ��B�Ĵ�С��$\frac{m{v}_{0}}{eL}$������ֱֽ�����⣻
��2��P�����������������ӵĶ���֮����5��1������С��ʱ����t��$\frac{����-2��L}{2{v}_{0}}$��
��3��OD�����Ϊ3L��
���� �������Ĺؼ���ץס�糡��ƫת��ų���ƫת�о������IJ�ͬ���ֱ������˶��ĺϳ���ֽ⼰Բ���˶����ɲ���϶���ѧ�������д�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
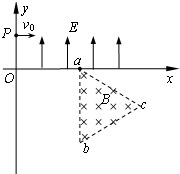 ��ͼ��ʾ��ƽ��ֱ������ϵxoy���ڵ�һ��������ƽ����y�����ǿ�糡��������y�������ڵ���������������abc����������ǿ�ų�������ֱ��xoyƽ������������α߳�ΪL����ab����y��ƽ�У�һ����Ϊm�������Ϊq�����ӣ���y���ϵ�p�㣨����0��h�����Դ�СΪv0���ٶ���x������������糡��ͨ���糡���x���ϵ�a�㣨2h��0������������ޣ������ų����ִ�y���ϵ�ij�����������ޣ����ٶ���y�Ḻ�����45��ǣ������������ܵ���������
��ͼ��ʾ��ƽ��ֱ������ϵxoy���ڵ�һ��������ƽ����y�����ǿ�糡��������y�������ڵ���������������abc����������ǿ�ų�������ֱ��xoyƽ������������α߳�ΪL����ab����y��ƽ�У�һ����Ϊm�������Ϊq�����ӣ���y���ϵ�p�㣨����0��h�����Դ�СΪv0���ٶ���x������������糡��ͨ���糡���x���ϵ�a�㣨2h��0������������ޣ������ų����ִ�y���ϵ�ij�����������ޣ����ٶ���y�Ḻ�����45��ǣ������������ܵ����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �綯����������ʱ�����빦��Ϊ1W | |
| B�� | �綯����������ʱ���������Ϊ4W | |
| C�� | �綯��ÿ���ܽ�����ת����4J�Ļ�е�� | |
| D�� | �綯����������ʱ�ĵ���ǿ��Ϊ1A |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
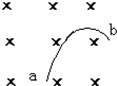 ��ͼ��ʾ��������ѷ�������У��д�ֱֽ���������ǿ�ų���ͼ������ab����һ����ֱ�ڴų���������Ĵ������ӵľ��������������н���ʹ��Χ������룬������Խ��ԽС���������ֲ��䣬�ɴ˿�֪��������
��ͼ��ʾ��������ѷ�������У��д�ֱֽ���������ǿ�ų���ͼ������ab����һ����ֱ�ڴų���������Ĵ������ӵľ��������������н���ʹ��Χ������룬������Խ��ԽС���������ֲ��䣬�ɴ˿�֪��������| A�� | ���Ӵ����磬��a��b�˶� | B�� | ���Ӵ����磬��b��a�˶� | ||
| C�� | ���Ӵ����磬��a��b�˶� | D�� | ���Ӵ����磬��b��a�˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
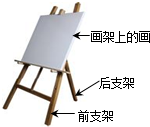 ��ͼ��ʾ��ˮƽ�����Ϸ���һ�����ܣ�����ǰ֧���ǹ̶�����֧�ܿ�ǰ���ƶ��������Ͼ�ֹ����һ����ΪG�Ļ�������˵����ȷ���ǣ�������
��ͼ��ʾ��ˮƽ�����Ϸ���һ�����ܣ�����ǰ֧���ǹ̶�����֧�ܿ�ǰ���ƶ��������Ͼ�ֹ����һ����ΪG�Ļ�������˵����ȷ���ǣ�������| A�� | ���ܶԻ�������������G | |
| B�� | ���ܶԻ�����������С����G | |
| C�� | ����֧�ܻ���������ܶԻ���������� | |
| D�� | ����֧�ܻ���������ܶԻ����������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 6s��24m | B�� | 6 s��25 m | C�� | 6.25 s��24 m | D�� | 6.25 s��25 m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ƽ��MN��PQ��STΪ�����ƽ�еĽ��棬��Ϊ���ֲ�ͬ�Ľ��ʣ�ƽ��ST���ϱ���Ϳ�з���㣨���߲���ͨ������ij�ֵ�ɫ�����������MN������һϵ�еķ������������·��ͼ��ʾ��������
ƽ��MN��PQ��STΪ�����ƽ�еĽ��棬��Ϊ���ֲ�ͬ�Ľ��ʣ�ƽ��ST���ϱ���Ϳ�з���㣨���߲���ͨ������ij�ֵ�ɫ�����������MN������һϵ�еķ������������·��ͼ��ʾ��������| A�� | ������Ǧ��ʵ���Сʱ������c��d�����ܻ���ʧ | |
| B�� | ������Ǧ��ʵ�����ʱ������d���ܻ���ʧ | |
| C�� | �������ֽ��ʣ����ڽ��ʢ��еĴ����ٶ���С | |
| D�� | �������b��c��d��һ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
| U/V | 0.00 | 2.56 | 2.71 | 2.80 | 2.84 | 2.87 | 2.89 | 2.91 | 2.99 |
| I/A | 0.00 | 0.03 | 0.07 | 0.11 | 0.34 | 0.52 | 0.75 | 0.91 | 3.02 |
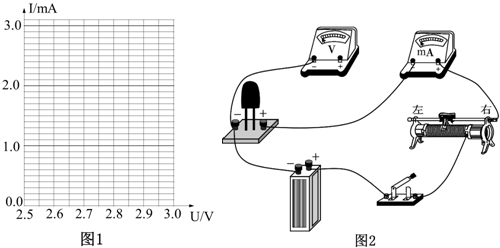
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com