
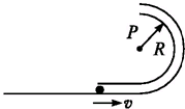
 如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:
如图所示,半径为R,内径很小的光滑半圆管道竖直放置,质量为m的小球以某一速度进入管内,小球通过最高点P时,对管壁的压力为0,已知重力加速度为g.求:分析 (1)小球通过最高点P时,对管壁的压力为0,重力恰好提供向心力,根据向心力公式即可求得小球从管口飞出时的速率;
(2)小球从管口飞出后做平抛运动,根据平抛运动的基本规律即可求解.
解答 解:(1)以小球为对象,设其到达最高点时的速度为vP,根据向心力公式有:$mg=\frac{m{v}_{P}^{2}}{R}$
代入解得:${v}_{P}=\sqrt{gR}$
(2)小球脱离轨道的最高点后做平抛运动,运动的时间:
t=$\sqrt{\frac{2•2R}{g}}=2\sqrt{\frac{R}{g}}$
所以小球的水平位移为:
X=${v}_{P}•t=\sqrt{gR}•2\sqrt{\frac{R}{g}}=2R$
答:(1)小球从管口飞出时的速率是$\sqrt{gR}$;
(2)小球落地点到P点的水平距离X是2R.
点评 本题是向心力知识和平抛运动的综合应用,注意受力分析时要注意弹力的方向,根据牛顿定律列出在最高点的方程;注意掌握平抛运动的规律及处理方法;此题是常规题,考试时不能失误.


科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若D表示某质点做匀速直线运动的位移,则$\frac{△D}{△t}$是恒定不变的 | |
| B. | 若D表示某质点的动能,$\frac{△D}{△t}$越大,则该质点所受外力做的总功就越多 | |
| C. | 若D表示某质点做平抛运动的速度,则$\frac{△D}{△t}$是恒定不变的 | |
| D. | 若D表示圆周运动转过的角度,则$\frac{△D}{△t}$是恒定不变的 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
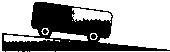 一辆质量为m的汽车,以恒定的输出功率P在倾角为θ的斜坡上沿坡匀速行驶,如图所示,汽车受到的摩擦阻力恒为f(忽略空气阻力).求:
一辆质量为m的汽车,以恒定的输出功率P在倾角为θ的斜坡上沿坡匀速行驶,如图所示,汽车受到的摩擦阻力恒为f(忽略空气阻力).求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两者轨道半径不同 | |
| B. | 两者向心加速度大小不同 | |
| C. | 两者运行速率相同 | |
| D. | 两者相对于地面上固定的观察者均静止 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
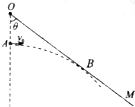 如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求:
如图所示,挡板OM与竖直方向所夹的锐角为θ,一小球(视为质点)从O点正下方和A点以速度v0水平抛出,小球运动过程中恰好不和挡板碰撞(小球轨迹所在平面与挡板垂直).不计空气阻力,重力加速度大小为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | a、b是光的干涉图样 | |
| B. | c、d是光的干涉图样 | |
| C. | 形成a图样光的波长比形成b图样光的波长短 | |
| D. | c、d中央条纹为暗纹 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
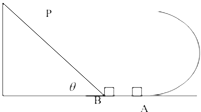 如图所示,在光滑水平地面上有一竖直固定的半径为R的光滑半圆弧轨道和一倾角为θ的表面光滑的斜面体,质量均为m的物体A和B分别放在圆弧轨道和斜面体的底端.
如图所示,在光滑水平地面上有一竖直固定的半径为R的光滑半圆弧轨道和一倾角为θ的表面光滑的斜面体,质量均为m的物体A和B分别放在圆弧轨道和斜面体的底端.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com