
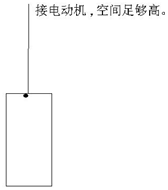
 实验用升降机箱体质量为M=55kg,内部天花板到地板间距恰好H=6m.某次实验时,开动电机给升降机箱体恒定的拉力使箱体匀加速上升,加速度大小为$\frac{1}{5}$g,静止启动的同时从天花板处让一弹性小球自由下落.已知小球质量m=5kg,小球和箱体只在竖直方向上运动且每次碰撞都是弹性碰撞,碰撞时间很短,内力远大于外力,忽略空气阻力,g取10m/s2.求:
实验用升降机箱体质量为M=55kg,内部天花板到地板间距恰好H=6m.某次实验时,开动电机给升降机箱体恒定的拉力使箱体匀加速上升,加速度大小为$\frac{1}{5}$g,静止启动的同时从天花板处让一弹性小球自由下落.已知小球质量m=5kg,小球和箱体只在竖直方向上运动且每次碰撞都是弹性碰撞,碰撞时间很短,内力远大于外力,忽略空气阻力,g取10m/s2.求:分析 (1)第一次碰撞前,小球做自由落体运动,箱体做匀加速运动,当两者位移这和等于H时第一次相碰,根据位移关系求时间.
(2)小球和箱体发生弹性碰撞,根据动量守恒定律和能量守恒定律列式,可求得第一次碰撞结束时箱体速度大小和小球的速度大小.
(3)用同样的方法求得小球和箱体第一次碰撞到第二次碰撞的时间,以及第二次与第三次碰撞经过的时间,求得箱体的总位移,由牛顿第二定律求出电机对箱体的拉力,从而求得电机对箱体做的功.
解答 解:(1)设t时间第一次相碰,由运动学规律得:
h球=$\frac{1}{2}g{t}^{2}$
h箱=$\frac{1}{2}a{t}^{2}$
且有:h球+h箱=H
解得:t=$\sqrt{\frac{2H}{g+a}}$
代入数据解得:t=1s,h球=1m
(2)碰撞前小球的速度为 v1=gt=10m/s(竖直向下)
箱体的速度为 v2=at=2m/s(竖直向上),设碰后小球速度为向上的v1′,箱体速度为向上的v2′.取向上为正方向,根据动量守恒定律和能量守恒定律得:
Mv2-mv1=mv1′+Mv2′
$\frac{1}{2}$Mv22+$\frac{1}{2}$mv12=$\frac{1}{2}$mv1′2+$\frac{1}{2}$Mv2′2.
可得:v1+v2=v1′-v2′
代入数据解得:v1′=12m/s,v2′=0
(3)经分析小球不会碰箱体天花板.设经时间t2第二次碰地板.
则 h2=v1′t2-$\frac{1}{2}g{t}_{2}^{2}$
h2=$\frac{1}{2}a{t}_{2}^{2}$
解得 t2=2s,h2=4m
可得第二次碰前速度小球为8m/s(向下),箱体为4m/s(向上)
同样,由碰撞中动量守恒和能量守恒可得:第二次碰后小球速度为v1″=14m/s(向上),箱体速度为 v2″=2m/s(向上).
计算判断小球还是不与天花板相撞.
设经时间t3第三次碰地板.
则 h3=v1″t3-=$\frac{1}{2}g{t}_{3}^{2}$
h3=v2″t3+$\frac{1}{2}a{t}_{3}^{2}$
解得 t3=2s,h3=8m
所以第三次碰前箱体上升的总高度为 S=h箱+h2+h3=13m
对箱体受力分析,有
F-Mg=Ma
得 F=660N
则电机对箱体做的功为 W=FS
解得 W=8580J
答:
(1)小球开始运动经1s长时间与箱体发生第一次碰撞.
(2)第一次碰撞结束时箱体速度大小和小球的速度大小分别为0和12m/s.
(3)从开始运动到第三次碰撞箱体前电机对箱体做的功是8580J.
点评 解决本题的关键之处在于理清小球和箱体的运动关系,把握位移间的位移,知道弹性碰撞遵守两大守恒定律:动量守恒定律和能量守恒定律,边计算边分析.


科目:高中物理 来源: 题型:选择题
 如图所示,在竖直平面内有一半径为R的四分之三圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,不计空气阻力,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2.5R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一半径为R的四分之三圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,不计空气阻力,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2.5R,重力加速度为g,则小球从P到B的运动过程中( )| A. | 重力做功1.5mgR | B. | 动能增加mgR | ||
| C. | 摩擦力做功mgR | D. | 离开B点后小球能落在圆轨道内 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )
如图所示,S是水面波的波源,MN是挡板,S1、S2是两个狭缝.已知两狭缝的宽度相等且比波长小得多,狭缝的开合可以控制.下列判断正确的是( )| A. | 若合上S1,只打开S2,则会看到水波隐定的干涉图样 | |
| B. | 若合上S1,只打开S2,则会看到水波的衍射现象 | |
| C. | 若S1、S2都打开,则会看到水波隐定的干涉图样 | |
| D. | 若S1、S2都打开,则会看到水波的衍射现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
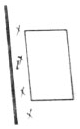 如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )
如图所示,矩形线圈位于通电长直导线附近,线圈与导线在同一平面内,通电直导线中电流i与时间t的关系有图A、B、C、D四种情况,在0~t0这段时间内,矩形线圈中有方向不变的感应电流的是( )| A. | 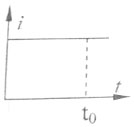 | B. | 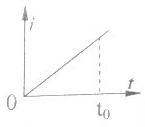 | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 衰变发出的γ射线是波长很短的光子,穿透能力很强 | |
| B. | 上述衰变方程中的X含有143个中子 | |
| C. | 8个$\left.\begin{array}{l}{239}\\{94}\end{array}\right.$Pu经过24100年后一定还剩余4个 | |
| D. | 衰变过程中总质量不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )
如图所示,一木块静置于光滑的水平面上,一颗子弹沿水平方向射入木块,若子弹进入木块的深度为x2,与此同时木块沿水平面移动了x1.设子弹在木块中受到的阻力大小不变,则在子弹进入木块的过程中( )| A. | 子弹损失的动能与木块获得的动能之比为(x1+x2):x1 | |
| B. | 子弹损失的动能与系统产生的内能之比为(x1+x2):x1 | |
| C. | 木块获得的动能与系统产生的内能之比为x1:x2 | |
| D. | 木块获得的动能与系统产生的内能之比为x2:x1 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,PQCD为光滑的轨道,其中PQ是水平的,CD是竖直平面内的圆轨道,与PQ相切于C点,且半径R=0.5m,圆轨道下端不重叠,物体可从水平轨道右侧运动冲上轨道,并从左侧离开轨道.质量m=0.1kg的A滑块静止在水平轨道上,另一质量M=0.5kg的B滑块前端装有以轻质弹簧(A、B均可视为质点),以速度v0向左运动并与滑块A发生弹性正碰,若相碰后A滑块能过半圆最高点D,取重力加速度g=10m/s2,则:
如图所示,PQCD为光滑的轨道,其中PQ是水平的,CD是竖直平面内的圆轨道,与PQ相切于C点,且半径R=0.5m,圆轨道下端不重叠,物体可从水平轨道右侧运动冲上轨道,并从左侧离开轨道.质量m=0.1kg的A滑块静止在水平轨道上,另一质量M=0.5kg的B滑块前端装有以轻质弹簧(A、B均可视为质点),以速度v0向左运动并与滑块A发生弹性正碰,若相碰后A滑块能过半圆最高点D,取重力加速度g=10m/s2,则:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com