
 如图所示,水平地面上有一个坑,其竖直截面为半圆,O为圆心,且AB为沿水平方向的直径,圆弧上有一点C,且∠BOC=60°.若在A点以初速度v0沿水平方向抛出一个质量为m的小球,小球将击中坑壁上的C点.重力加速度为g,圆的半径为R,下列说法正确的是( )
如图所示,水平地面上有一个坑,其竖直截面为半圆,O为圆心,且AB为沿水平方向的直径,圆弧上有一点C,且∠BOC=60°.若在A点以初速度v0沿水平方向抛出一个质量为m的小球,小球将击中坑壁上的C点.重力加速度为g,圆的半径为R,下列说法正确的是( )| A. | 小球击中C点时速度与水平方向的夹角为30° | |
| B. | 小球飞行的时间为$\frac{{2\sqrt{3}{V_0}}}{3g}$ | |
| C. | 只要速度v0与R满足一定的关系,小球在C点能垂直击中圆弧 | |
| D. | 不论v0取多大值,小球都不可能在C点垂直击中圆弧 |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式求出小球飞行的时间.抓住小球某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,分析小球能否垂直击中C点.
解答 解:A、小球击中C点时,竖直位移y=$Rsin60°=\frac{\sqrt{3}}{2}R$,水平位移x=$R+Rcos60°=\frac{3}{2}R$,位移与水平方向夹角的正切值$tanα=\frac{y}{x}=\frac{\frac{\sqrt{3}R}{2}}{\frac{3R}{2}}=\frac{\sqrt{3}}{3}$,平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,即$tanα=\frac{2\sqrt{3}}{3}$,速度与水平方向夹角$α=arctan\frac{2\sqrt{3}}{3}$,故A错误.
B、小球的飞行时间t=$\frac{x}{{v}_{0}}=\frac{3R}{2{v}_{0}}$,根据$y=\frac{1}{2}g{t}^{2}$,x=v0t得,$4\sqrt{3}{{v}_{0}}^{2}=9gR$,则$t=\frac{3R}{2{v}_{0}}=\frac{2\sqrt{3}{v}_{0}}{3g}$,故B正确.
C、若小球在C点垂直击中圆弧,则速度的反向延长线经过圆心,根据几何关系知,速度与水平方向的夹角是位移与水平方向夹角的2倍,由于平抛运动某时刻速度方向与水平方向夹角的正切值是位移与水平方向夹角正切值的2倍,所以小球不可能在C点垂直击中圆弧,故C错误,D正确.
故选:BD.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解,难度中等.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示为赛车场的一个水平“U“表、形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,(X)′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大).求:
如图所示为赛车场的一个水平“U“表、形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,(X)′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大).求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,足够长的光滑金属框竖直放置,框宽l=0.5m,框的电阻不计,匀强磁场的磁感应强度B=1T,方向与框面垂直,金属棒MN的质量为100g,电阻为1Ω,现让MN由静止释放,MN与金属框始终垂直并保持良好接触,从释放直至达到最大速度的过程中通过金属棒某一截面的电荷量为2C,求:(空气阻力不计,g取10m/s2)
如图所示,足够长的光滑金属框竖直放置,框宽l=0.5m,框的电阻不计,匀强磁场的磁感应强度B=1T,方向与框面垂直,金属棒MN的质量为100g,电阻为1Ω,现让MN由静止释放,MN与金属框始终垂直并保持良好接触,从释放直至达到最大速度的过程中通过金属棒某一截面的电荷量为2C,求:(空气阻力不计,g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,在空间中取直角坐标系Oxy,在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,MN为电场的理想边界,场强大小为E.ON=d.电子从y轴上的A点以初速度v0沿x轴正方向射入电场区域,从MN上的P点离开电场.已知A点坐标为(0,h),电子的电量为e,质量为m,电子的重力忽略不计,求:
如图所示,在空间中取直角坐标系Oxy,在第一象限内从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,MN为电场的理想边界,场强大小为E.ON=d.电子从y轴上的A点以初速度v0沿x轴正方向射入电场区域,从MN上的P点离开电场.已知A点坐标为(0,h),电子的电量为e,质量为m,电子的重力忽略不计,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 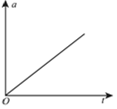 | B. | 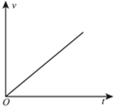 | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | t1=t2 | B. | t1>t2 | C. | t1<t2 | D. | 不能确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 在用如图所示装置做“探究功与速度变化的关系”的实验时,除了图中已有的实验器材外,还需要导线、开关、刻度尺和交流电源(填”交流”或”直流”);下列说法中正确AD
在用如图所示装置做“探究功与速度变化的关系”的实验时,除了图中已有的实验器材外,还需要导线、开关、刻度尺和交流电源(填”交流”或”直流”);下列说法中正确AD 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com