
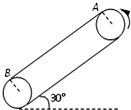
 如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度?
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=$\frac{1}{4π}$m,两轮轴心相距L=8.15m,A、B分别使传送带与两轮的切点,轮缘与传送带之间不打滑,一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ=$\frac{\sqrt{3}}{6}$.小物块相对于传送带运动时,会在传送带上留下痕迹.当传送带沿逆时针方向匀速运动时,小物块无初速地放在A点,运动至B点飞出.若传送带沿逆时针方向匀速运动的速度v0=1.5m/s,求划痕的长度? 分析 根据牛顿第二定律,抓住物体相对滑动所受的摩擦力沿斜面向下,求出匀加速运动的加速度的大小.根据运动学公式求出速度达到传送带速度时的时间和位移,根据牛顿第二定律求出继续做匀加速运动的加速度,根据位移时间公式求出继续匀加速运动的时间,物体速度达到传送带前相对传送带向上滑,速度达到传送带速度后相对传送带向下滑,结合相对位移的大小关系确定最终的相对位移大小,即痕迹的长度.
解答 解:物体开始阶段匀加速下滑,根据牛顿第二定律得其加速度为:
a1=$\frac{mgsin30°+μmgcos30°}{m}$=gsin30°+μgcos30°=5+$\frac{\sqrt{3}}{6}$×10×$\frac{\sqrt{3}}{2}$=7.5m/s2.
物体速度达到传送带速度的时间为:
t1=$\frac{{v}_{0}}{{a}_{1}}$=$\frac{1.5}{7.5}$s=0.2s,
运动的位移为:
x1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}$=$\frac{1}{2}×7.5×0.{2}^{2}$m=0.15m.
速度达到传送带速度后,由于mgsin30°>μmgcos30°,所以物体继续做匀加速直线运动,加速度为:
a2=$\frac{mgsin30°-μmgcos°}{m}$=gsin30°-μgcos30°=5-$\frac{\sqrt{3}}{6}$×10×$\frac{\sqrt{3}}{2}$=2.5m/s2.
根据L-x1=v0t2+$\frac{1}{2}$a2t22代入数据得:t2=2s
物体速度达到传送带速度前,相对滑动的位移为:
△x1=v2t1-x1=1.5×0.2m-0.15m=0.15m,
达到传送带速度后相对滑动的位移大小为:
△x2=x2-v0t2=8.15-0.15-1.5×2m=5m,
可知相对滑动的位移为:△x=△x1+△x2=5.15m,则划痕的长度为5.15m.
答:划痕的长度为5.15m.
点评 解决本题的关键理清物体在传送带上整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,要注意划痕的长度等于物体与传送带间的相对位移大小,不等于物体相对于地的位移大小.


科目:高中物理 来源: 题型:多选题
 2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )
2011年3月10日12时58分云南盈江发生了5.8级地震.在抗震救灾中,我国自主研制的“北斗一号“卫星导航系统,在抗震救灾中发挥了巨大作用.北斗导航系统又被称为“双星定位系统“,具有导航、定位等功能.“北斗“系统中两颗工作星均绕地心O做匀速圆周运动,轨道半径为r,某时刻两颗工作卫星分别位于轨道上的AB两位置 (如图所示).若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则下列判断中正确的是( )| A. | 这两颗卫星的加速度大小相等,均为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动至位置B所需的时间为$\frac{πr}{R}$$\sqrt{\frac{r}{g}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 要测量一个量程已知的电压表的内阻,所备器材如下:
要测量一个量程已知的电压表的内阻,所备器材如下:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 一同学用多用表测量一定值电阻的阻值大小,当他选用欧姆档×100档后,调零后测量该电阻,指针指在如图所示的虚线位置,之后他调整选择开关到合适的临近一档,调零后测量该电阻,指针指在如图所示的实线位置,则此固定电阻的阻值大小为320Ω.
一同学用多用表测量一定值电阻的阻值大小,当他选用欧姆档×100档后,调零后测量该电阻,指针指在如图所示的虚线位置,之后他调整选择开关到合适的临近一档,调零后测量该电阻,指针指在如图所示的实线位置,则此固定电阻的阻值大小为320Ω.查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | h1>h2 | |
| B. | h1=h2 | |
| C. | h1<h2 | |
| D. | h1,h2的大小关系与两个物体的质量有关 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在距地面高h=0.8m处,将一小球A以初速度v0=2m/s水平向右抛出,与此同时,在A球的正下方的水平地面上有一质量m=0.2kg的滑块B在一水平向右的恒定拉力的作用下由静止加速滑出,结果A、B恰好相碰.已知滑块B与地面的动摩擦因数μ=0.5,A、B均可看作质点,空气阻力不计,取g=10m/s2.试求:
如图所示,在距地面高h=0.8m处,将一小球A以初速度v0=2m/s水平向右抛出,与此同时,在A球的正下方的水平地面上有一质量m=0.2kg的滑块B在一水平向右的恒定拉力的作用下由静止加速滑出,结果A、B恰好相碰.已知滑块B与地面的动摩擦因数μ=0.5,A、B均可看作质点,空气阻力不计,取g=10m/s2.试求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在该星球表面上以$\sqrt{\frac{2{v}_{0}R}{t}}$的初速度水平抛出一个物体,物体将不再落回星球表面 | |
| B. | 在该星球表面上以2$\sqrt{\frac{{v}_{0}R}{t}}$的初速度水平抛出一个物体,物体将不再落回星球表面 | |
| C. | 在该星球表面上以2$\sqrt{\frac{{v}_{0}R}{t}}$的初速度竖直抛出一个物体,物体将不再落回星球表面 | |
| D. | 在该星球表面上以 $\sqrt{\frac{2{v}_{0}R}{t}}$的初速度竖直抛出一个物体,物体将不再落回星球表面 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连.已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面的匀强磁场(图中未画出)中.若断开开关S,将一根质量为m、电阻为r、长也为L的金属棒从AA′处静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,将金属棒仍从AA′处静止开始滑下,则金属棒落地点离PP′的水平距离为x2.不计导轨电阻,忽略金属棒经过PP′处的能量损失,已知重力加速度为g,求:
如图所示,宽度为L的粗糙平行金属导轨PQ和P′Q′倾斜放置,顶端QQ′之间连接一个阻值为R的电阻和开关S,底端PP′处与一小段水平轨道用光滑圆弧相连.已知底端PP′离地面的高度为h,倾斜导轨处于垂直于导轨平面的匀强磁场(图中未画出)中.若断开开关S,将一根质量为m、电阻为r、长也为L的金属棒从AA′处静止开始滑下,金属棒落地点离PP′的水平距离为x1;若闭合开关S,将金属棒仍从AA′处静止开始滑下,则金属棒落地点离PP′的水平距离为x2.不计导轨电阻,忽略金属棒经过PP′处的能量损失,已知重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 放在粗糙水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间的图象和拉力的功率与时间的图象如图所示.下列说法正确的是( )
放在粗糙水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间的图象和拉力的功率与时间的图象如图所示.下列说法正确的是( )| A. | 物体的质量为$\frac{10}{9}$kg | B. | 滑动摩擦力的大小为5N | ||
| C. | 0~6s内物体的位移大小为24m | D. | 0~2s内拉力做的功为20J |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com