
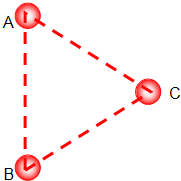
 三个质量分布均匀的小球A、B、C,质量依次为m、m、2m.这三个小球被固定在边长为L的正三角形的顶点上(球心与顶点重合).求:
三个质量分布均匀的小球A、B、C,质量依次为m、m、2m.这三个小球被固定在边长为L的正三角形的顶点上(球心与顶点重合).求:分析 (1)先求A、B两个小球单独对C球的万有引力,再根据平行四边形定则合成
(2)先求A、C两球单独对B球的万有引力,再运用正交分解法求合力
解答 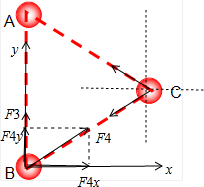 解:(1)A对C的万有引力${F}_{1}^{\;}=G\frac{m•2m}{{L}_{\;}^{2}}=\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
解:(1)A对C的万有引力${F}_{1}^{\;}=G\frac{m•2m}{{L}_{\;}^{2}}=\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
B对C的万有引力为${F}_{2}^{\;}=G\frac{m•2m}{{L}_{\;}^{2}}=\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
A、B对C球的万有引力大小为$F={F}_{1}^{\;}cos30°+{F}_{2}^{\;}cos30°=\frac{2\sqrt{3}G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
(2)A对B的万有引力为:${F}_{3}^{\;}=G\frac{{m}_{\;}^{2}}{{L}_{\;}^{2}}$
C对B的万有引力为:${F}_{4}^{\;}=G\frac{m•2m}{{L}_{\;}^{2}}=\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
将${F}_{3}^{\;}、{F}_{4}^{\;}$沿水平和竖直方向正交分解,如图所示
${F}_{4x}^{\;}={F}_{4}^{\;}cos30°=\frac{\sqrt{3}G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
${F}_{4y}^{\;}={F}_{4}^{\;}sin30°=\frac{G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
竖直方向合力${F}_{y}^{\;}={F}_{3}^{\;}+{F}_{4Y}^{\;}=\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
水平方向的合力${F}_{x}^{\;}={F}_{4x}^{\;}=\frac{\sqrt{3}G{m}_{\;}^{2}}{{L}_{\;}^{2}}$
A、C对B的万有引力${F}_{B}^{\;}=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}=\sqrt{7}G\frac{{m}_{\;}^{2}}{{L}_{\;}^{2}}$
答:(1)A、B对C球的万有引力大小为$\frac{2G{m}_{\;}^{2}}{{L}_{\;}^{2}}$;
(2)A、C对B球的万有引力大小为$\sqrt{7}G\frac{{m}_{\;}^{2}}{{L}_{\;}^{2}}$
点评 本题考查万有引力的叠加,根据力的独立作用原理,根据万有引力定律求出每个小球受到其他小球的引力,画出受力分析图,采用合成法或正交分解法求出合力.


科目:高中物理 来源: 题型:选择题
| A. | 根据速度的定义式,当△t非常小时,就可以用平均速度表示物体在t时刻的瞬时速度,该定义运用了微元法 | |
| B. | 在不需要考虑物体本身的形状和大小时,用质点来代替物体的方法叫假设法 | |
| C. | 在用打点计时器研究自由落体运动时,把重物在空气中的落体运动近似看做自由落体运动,这里采用了控制变量法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
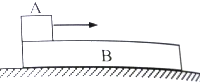 质量为m的滑块A的速度v沿水平方向滑到静止于水平光滑平面上足够长的物体B上,B的质量为M,AB间动摩擦因数为μ,问A在B上滑行多远时A相对B静止.
质量为m的滑块A的速度v沿水平方向滑到静止于水平光滑平面上足够长的物体B上,B的质量为M,AB间动摩擦因数为μ,问A在B上滑行多远时A相对B静止.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
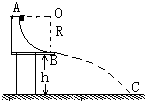 如图所示,在竖直平面内有$\frac{1}{4}$圆弧形轨道AB,其半径为1m,B点的切线恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A由静止开始沿轨道滑下,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点,若轨道B端距地面高为h=5m,不计空气阻力,取g=10m/s2,求:
如图所示,在竖直平面内有$\frac{1}{4}$圆弧形轨道AB,其半径为1m,B点的切线恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A由静止开始沿轨道滑下,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点,若轨道B端距地面高为h=5m,不计空气阻力,取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 铀核裂变的核反应是:${\;}_{92}^{235}$U→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+2${\;}_{0}^{1}$n | |
| B. | α粒子散射实验可以用来确定原子核电荷量和估算原子核半径 | |
| C. | 氢原子辐射出一个光子后能量减小,核外电子的运动加速度减小 | |
| D. | 比结合能越大,表示原子核中核子结合得越牢靠,原子核越稳定 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,细绳一端系着质量M=0.6kg的物体,静止在水平面上,另一端通过光滑的小孔吊着质量m=0.3kg的物体,M的中点与圆孔的距离为r=1m,现在物体M随盘绕中心轴匀速转动角速度ω为2rad/s,求此时M与盘之间的静摩擦力大小与方向?(g取10m/s2)
如图所示,细绳一端系着质量M=0.6kg的物体,静止在水平面上,另一端通过光滑的小孔吊着质量m=0.3kg的物体,M的中点与圆孔的距离为r=1m,现在物体M随盘绕中心轴匀速转动角速度ω为2rad/s,求此时M与盘之间的静摩擦力大小与方向?(g取10m/s2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com